Tab og spændingsfald - hvad er forskellene

I det almindelige menneskeliv bruges ordene "tab" og "fald" til at betegne kendsgerningen om et fald i visse præstationer, men de betyder en anden værdi.

I dette tilfælde betyder "tab" tab af en del, beskadigelse, reduktion af størrelsen af ​​det tidligere opnåede niveau. Tab er uønskede, men du kan tåle dem.

Ordet "fald" forstås som en mere alvorlig skade forbundet med en fuldstændig fratagelse af rettigheder. Således kan selv lejlighedsvis forekommende tab (f.eks. en portefølje) over tid føre til et fald (f.eks. niveauet af den materielle levetid).

I denne henseende vil vi overveje dette spørgsmål i forhold til spændingen på det elektriske netværk.

Hvordan tab og spændingsfald dannes

Elektricitet transporteres over lange afstande af luftledninger fra en transformerstation til en anden.

Luftledninger er designet til at overføre den tilladte effekt og er lavet af metaltråde af et bestemt materiale og sektion. De skaber en resistiv belastning med en modstandsværdi på R og en reaktiv belastning på X.

På den modtagende side står den transformerelkonvertering.Dens spoler har en aktiv og udtalt induktiv modstand XL. Den sekundære side af transformeren sænker spændingen og sender den videre til forbrugerne, hvis belastning er udtrykt ved værdien af ​​Z og er aktiv, kapacitiv og induktiv af natur. Dette påvirker også netværkets elektriske parametre.

Spændingen påført ledningerne til understøtningen af ​​luftledningen, tættest på krafttransmissionstransformatorstationen, overvinder den reaktive og aktive modstand af kredsløbet i hver fase og skaber en strøm i den, hvis vektor afviger fra vektorens vektor. påført spænding med en vinkel φ.

Arten af ​​fordelingen af ​​spændinger og strømmen af ​​strømme langs linjen for en symmetrisk belastningstilstand er vist på billedet.

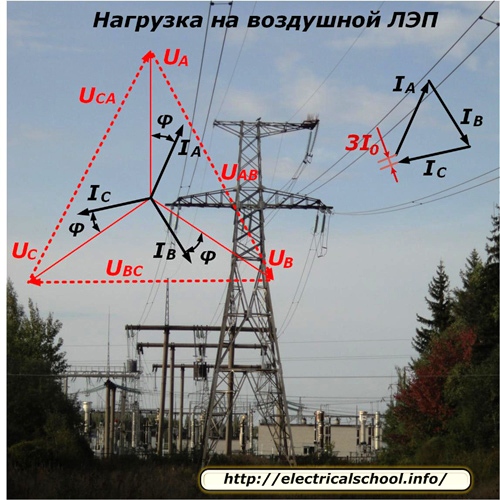
Da hver fase af linjen fodrer et forskelligt antal forbrugere, som også er tilfældigt afbrudt eller tilsluttet arbejde, er det teknisk meget vanskeligt at afbalancere fasebelastningen perfekt. Der er altid en ubalance i den, som er bestemt af vektortilsætningen af ​​fasestrømmene og skrevet som 3I0. I de fleste beregninger ignoreres det simpelthen.

Den energi, der forbruges af den transmitterende understation, bruges delvist på at overvinde ledningens modstand og når den modtagende side med ringe ændring. Denne fraktion er karakteriseret ved tab og spændingsfald, hvis vektor aftager lidt i amplitude og forskydes med en vinkel i hver fase.

Hvordan tab og spændingsfald beregnes

For at forstå de processer, der finder sted under transmissionen af ​​elektricitet, er vektorformen praktisk til at repræsentere hovedegenskaberne. Forskellige matematiske beregningsmetoder er også baseret på denne metode.

For at forenkle beregningerne i trefaset system det er repræsenteret af tre enfasede ækvivalente kredsløb. Denne metode fungerer godt med en symmetrisk belastning og giver dig mulighed for at analysere processerne, når den er brudt.

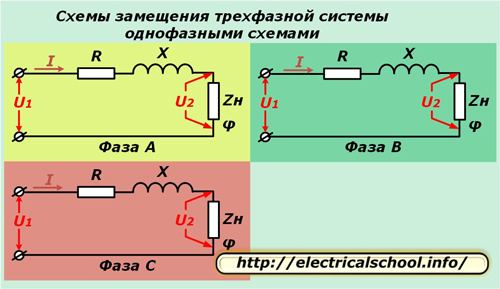
I ovenstående diagrammer er den aktive R og reaktans X for hver leder af linjen forbundet i serie med den komplekse belastningsmodstand Zn karakteriseret ved vinklen φ.

Derudover udføres beregning af spændingstab og spændingsfald i én fase. For at gøre dette skal du angive dataene. Til dette formål vælges en understation, der modtager energi, hvor den tilladte belastning allerede skal være fastlagt.

Spændingsværdien af ​​ethvert højspændingssystem er allerede angivet i referencebøgerne, og ledningernes modstande bestemmes af deres længde, tværsnit, materiale og netværkskonfiguration. Den maksimale strøm i kredsløbet er indstillet og begrænset af ledningernes egenskaber.

For at starte beregningerne har vi derfor: U2, R, X, Z, I, φ.

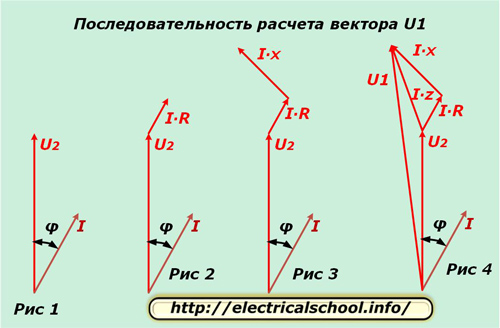
Vi tager en fase, for eksempel «A» og adskiller for den i det komplekse plan vektorerne U2 og I, forskudt med en vinkel φ, som vist i figur 1. Potentialeforskellen i lederens aktive modstand falder sammen i retningen med strømmen og i størrelse bestemmes ud fra udtrykket I ∙ R. Vi udskyder denne vektor fra slutningen af ​​U2 (fig. 2).

Potentialeforskellen i lederens reaktans adskiller sig fra strømmens retning med en vinkel φ1 og beregnes ud fra produktet I ∙ X. Vi udsætter det fra vektoren I ∙ R (fig. 3).

Påmindelser: For den positive rotationsretning af vektorerne i det komplekse plan tages bevægelsen mod uret. Strømmen, der strømmer gennem den induktive belastning, forsinker den påførte spænding med en vinkel.

Figur 4 viser afbildningen af ​​potentialedifferensvektorerne på den samlede ledningsmodstand I ∙ Z og spændingen ved indgangen til kredsløbet U1.

Nu kan du sammenligne inputvektorerne med det tilsvarende kredsløb og på tværs af belastningen. For at gøre dette skal du sætte det resulterende diagram vandret (fig. 5) og tegne en bue fra begyndelsen med radius af modulet U1, indtil det skærer retningen af ​​vektoren U2 (fig. 6).

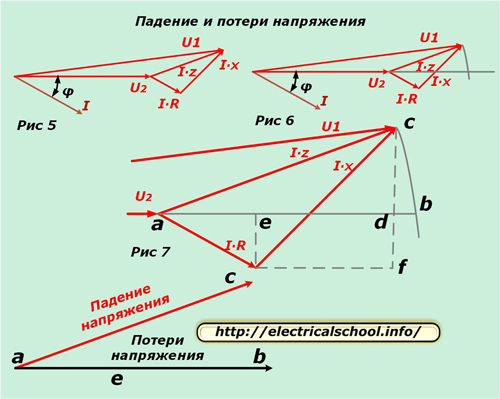
Figur 7 viser en forstørrelse af trekanten for større klarhed og tegning af hjælpelinjer, der angiver de karakteristiske skæringspunkter med bogstaver.

Nederst på billedet er det vist, at den resulterende vektor ac kaldes spændingsfaldet og ab kaldes tabet. De adskiller sig i størrelse og retning. Hvis vi vender tilbage til den oprindelige skala, vil vi se, at ac opnås som et resultat af geometrisk subtraktion af vektorer (U2 fra U1), og ab er aritmetisk. Denne proces er vist på billedet nedenfor (fig. 8).

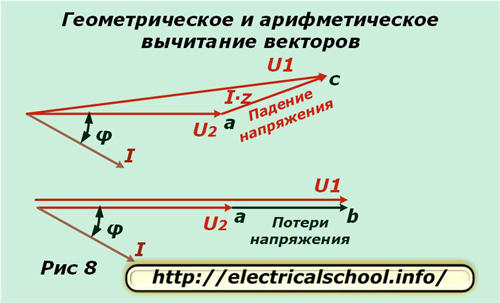
Udledning af formler til beregning af spændingstab

Lad os nu gå tilbage til figur 7 og bemærke, at bd-segmentet er meget lille. Af denne grund negligeres det i beregningerne, og spændingstabet beregnes ud fra segmentlængden ad. Den består af to linjestykker ae og ed.

Da ae = I ∙ R ∙ cosφ og ed = I ∙ x ∙ sinφ, så kan spændingstab for en fase beregnes med formlen:

∆Uph = I ∙ R ∙ cosφ + I ∙ x ∙ sinφ

Hvis vi antager, at belastningen er symmetrisk i alle faser (betinget negligering af 3I0), kan vi bruge matematiske metoder til at beregne spændingstabet i ledningen.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Hvis højre side af denne formel multipliceres og divideres med netværksspændingen Un, så får vi en formel, der giver os mulighed for at udføre pBeregning af spændingstab gennem strømforsyningen.

∆Ul = (P ∙ r + Q ∙ x) / Un

Værdierne for aktiv P og reaktiv Q-effekt kan tages fra linjemåleraflæsninger.

Spændingstabet i et elektrisk kredsløb afhænger således af:

• aktiv og reaktans af kredsløbet;

• komponenter af anvendt strøm;

• størrelsen af ​​den påførte spænding.

Udledning af formler til beregning af den tværgående komponent af spændingsfaldet

Lad os gå tilbage til figur 7. Værdien af ​​vektoren ac kan repræsenteres ved hypotenusen af ​​en retvinklet trekant acd. Vi har allerede beregnet annoncefoden. Lad os bestemme den tværgående komponent cd.

Figuren viser, at cd = cf-df.

df = ce = I ∙ R ∙ sin φ.

cf = I ∙ x ∙ cos φ.

cd = I ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Ved hjælp af de opnåede modeller udfører vi små matematiske transformationer og opnår den tværgående komponent af spændingsfaldet.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Bestemmelse af formlen til beregning af spændingen U1 i begyndelsen af ​​spændingsledningen

Ved at kende værdien af ​​spændingen for enden af ​​linjen U2, tabet ∆Ul og den tværgående komponent af dråbet δU, kan vi beregne værdien af ​​vektoren U1 ved Pythagoras sætning. I udvidet form har den følgende form.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Praktisk brug

Beregningen af ​​spændingstab udføres af ingeniører på stadiet med at skabe et elektrisk kredsløbsprojekt for det optimale valg af netværkets konfiguration og dets bestanddele.

Under driften af ​​elektriske installationer kan der om nødvendigt udføres samtidige målinger af spændingsvektorerne ved enderne af ledningerne periodisk, og resultaterne opnået ved metoden med enkle beregninger kan sammenlignes. Denne metode er velegnet til enheder, der er steget krav på grund af behovet for høj arbejdsnøjagtighed.

Spændingstab i sekundære kredsløb

Et eksempel er de sekundære kredsløb af målespændingstransformatorer, som nogle gange når flere hundrede meter i længden og transmitteres af et specielt strømkabel med et øget tværsnit.

De elektriske egenskaber af et sådant kabel er underlagt øgede krav til kvaliteten af ​​spændingstransmission.

Moderne beskyttelse af elektrisk udstyr kræver drift af målesystemer med høje metrologiske indikatorer og en nøjagtighedsklasse på 0,5 eller endda 0,2. Derfor skal tab af den spænding, der påføres dem, overvåges og tages i betragtning. Ellers kan den fejl, som de indfører i driften af ​​udstyret, påvirke alle operationelle egenskaber betydeligt.

Spændingstab i lange kabelledninger

Funktionen ved designet af det lange kabel er, at det har en kapacitiv modstand på grund af det ret tætte arrangement af ledende kerner og et tyndt lag isolering mellem dem. Den afbøjer yderligere den strømvektor, der passerer gennem kablet, og ændrer dens størrelse.

Effekten af ​​spændingsfald på kapacitiv modstand skal tages i betragtning i beregningen for at ændre værdien af ​​I ∙ z. Ellers ændres teknologien beskrevet ovenfor ikke.

Artiklen giver eksempler på tab og spændingsfald på luftledninger og kabler. De findes dog hos alle forbrugere af elektricitet, herunder elektriske motorer, transformere, induktorer, kondensatorbanker og andre enheder.

Mængden af ​​spændingstab for hver type elektrisk udstyr er lovligt reguleret med hensyn til driftsforhold, og princippet om deres bestemmelse i alle elektriske kredsløb er det samme.