Trekanter af spændinger, modstande og kræfter

Enhver, der har en idé om vektordiagrammer, vil let bemærke, at en retvinklet spændingstrekant kan skelnes meget tydeligt på dem, hvor hver side afspejler: kredsløbets samlede spænding, spændingen af ​​den aktive modstand og spændingen på reaktans.

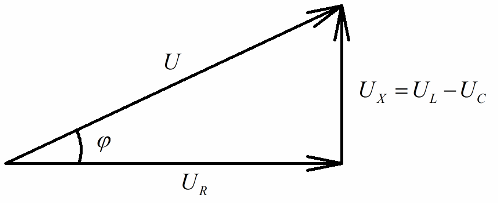
I overensstemmelse med Pythagoras sætning vil forholdet mellem disse spændinger (mellem den samlede spænding af kredsløbet og spændingen af ​​dets sektioner) se sådan ud:

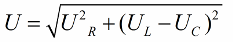
Hvis næste trin er at dividere værdierne af disse spændinger med strømmen (strømmen løber ligeligt gennem alle sektioner af seriekredsløbet), så ved Ohms lov vi får modstandsværdierne, det vil sige nu kan vi tale om en retvinklet trekant af modstande:

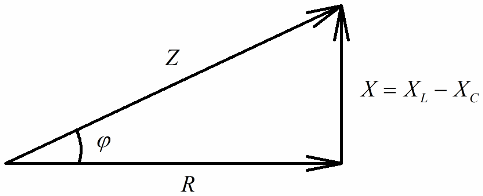
På lignende måde (som i tilfældet med spændinger), ved hjælp af Pythagoras sætning, er det muligt at etablere en sammenhæng mellem kredsløbets impedans og reaktanserne. Forholdet vil blive udtrykt ved følgende formel:

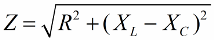
Derefter multiplicerer vi modstandsværdierne med strømmen, faktisk vil vi øge hver side af den retvinklede trekant med et vist antal gange. Som et resultat får vi en retvinklet trekant med kapaciteter:

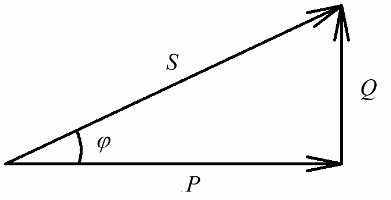
Den aktive effekt, der frigives ved den aktive modstand af kredsløbet, der er forbundet med den irreversible omdannelse af elektrisk energi (til varme, i udførelsen af ​​arbejde i installationen) vil være klart relateret til den reaktive effekt, der er involveret i den reversible omdannelse af energi (skabelsen) af magnetiske og elektriske felter i spoler og kondensatorer) og med fuld effekt leveret til den elektriske installation.

Aktiv effekt måles i watt (W), reaktiv effekt - i varis (VAR - volt-ampere reaktiv), total - i VA (volt-ampere).

Ifølge Pythagoras sætning har vi ret til at skrive:

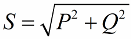
Lad os nu være opmærksomme på, at der i potenstrekanten er en vinkel phi, hvis cosinus er let at bestemme primært ved aktiv effekt og tilsyneladende kraft. Cosinus for denne vinkel (cos phi) kaldet effektfaktor. Den viser, hvor stor en del af den samlede effekt, der står for, når der udføres nyttigt arbejde i en el-installation og ikke føres tilbage til nettet.

En højere effektfaktor (maksimalt én) indikerer naturligvis en højere konverteringseffektivitet af den energi, der leveres til anlægget til drift. Hvis effektfaktoren er 1, så bruges al den tilførte energi til at udføre arbejde.

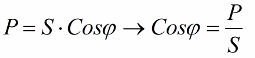
De opnåede forhold tillader udtrykket af installationens strømforbrug i form af effektfaktor, aktiv effekt og netværksspænding:

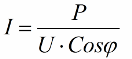
Så jo mindre cosinus phi, jo mere strøm kræves der af netværket for at udføre et bestemt job. I praksis begrænser denne faktor (maksimal netværksstrøm) transmissionskapaciteten af ​​transmissionslinjen, og jo lavere effektfaktoren er, jo større er linjebelastningen og jo lavere er den nyttige båndbredde (den lave cosinus phi fører til begrænsning). Joule-tab i kraftledninger med faldende cosinus phi kan ses ud fra følgende formel:

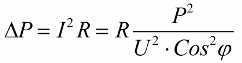
På transmissionsledningens aktive modstand R stiger tabene jo mere jo højere strøm I er, selvom den er reaktiv over for belastningen. Derfor kan vi sige, at med en lav effektfaktor stiger omkostningerne ved eltransmission simpelthen. Det betyder, at forøgelse af cosinus phi er en vigtig nationaløkonomisk opgave.

Det er ønskeligt, at den reaktive komponent af den samlede effekt nærmer sig nul. For at gøre dette ville det være godt altid at bruge elektriske motorer og transformere ved fuld belastning og slukke for dem ved afslutningen af ​​brugen, så de ikke går i tomgang. Ved ubelastet belastning har motorer og transformere en meget lav effektfaktor. En måde at øge cosinus phi hos brugere er at bruge kondensator banker og synkrone kompensatorer.