Aktiv modstand og induktor i AC-kredsløb

I betragtning af et AC-kredsløb, der kun indeholder induktiv modstand (se artiklen "Induktor i et vekselstrømkredsløb"), antog vi, at den aktive modstand af dette kredsløb er nul.

Faktisk har både selve spolens ledning og forbindelsesledningerne en lille, men aktiv modstand, så kredsløbet forbruger uundgåeligt strømkildens energi.

Derfor, når man bestemmer den samlede modstand af et eksternt kredsløb, er det nødvendigt at tilføje dets reaktive og aktive modstande. Men det er umuligt at tilføje disse to modstande, som er forskellige af natur.

I dette tilfælde findes kredsløbets impedans til vekselstrømmen ved geometrisk addition.

En retvinklet trekant (se figur 1) er konstrueret, hvor den ene side er værdien af ​​den induktive modstand, og den anden side er værdien af ​​den aktive modstand. Den ønskede kredsløbsimpedans bestemmes af trekantens tredje side.

Figur 1. Bestemmelse af impedansen af ​​et kredsløb indeholdende induktiv og aktiv modstand

Kredsløbsimpedans er angivet med det latinske bogstav Z og måles i ohm. Det ses af konstruktionen, at den samlede modstand altid er større end den induktive og aktive modstand taget hver for sig.

Det algebraiske udtryk for den samlede kredsløbsmodstand er:

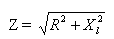
hvor Z - total modstand, R - aktiv modstand, XL - induktiv modstand af kredsløbet.

Derfor er den samlede modstand af et kredsløb til vekselstrøm, bestående af aktiv og induktiv modstand, lig med kvadratroden af ​​summen af ​​kvadraterne af den aktive og induktive modstand i dette kredsløb.

Ohms lov da et sådant kredsløb er udtrykt ved formlen I = U / Z, hvor Z er kredsløbets samlede modstand.

Lad os nu analysere, hvad spændingen bliver, hvis kredsløbet udover og og faseforskydningen mellem strømmen og induktansen også har en relativt stor aktiv modstand. I praksis kan et sådant kredsløb for eksempel være et kredsløb, der indeholder en jernkerne-induktor viklet af en tynd ledning (højfrekvent drossel).

I dette tilfælde vil faseforskydningen mellem strøm og spænding ikke længere være en fjerdedel af en periode (som det var i et kredsløb med kun induktiv modstand), men meget mindre; og jo større modstand, jo mindre faseforskydning vil der opstå.

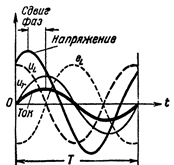
Figur 2. Strøm og spænding i et kredsløb, der indeholder R og L.

Nu er hun selv EMF af selvinduktion er ikke i modfase med den aktuelle kildespænding, da den er forskudt i forhold til spændingen ikke med en halv periode, men med mindre.Derudover er spændingen skabt af strømkilden ved spolens terminaler ikke lig med emf af selvinduktion, men er større end den med mængden af ​​spændingsfaldet i spoleledningens aktive modstand. Med andre ord består spændingen i spolen alligevel af to komponenter:

• tiL- den reaktive komponent af spændingen, som afbalancerer effekten af ​​EMF fra selvinduktion,

• tiR- den aktive komponent af spændingen, der vil overvinde kredsløbets aktive modstand.

Hvis vi forbinder en stor aktiv modstand i serie med spolen, vil faseforskydningen falde så meget, at den aktuelle sinusbølge næsten vil hamle op med spændingssinusbølgen, og forskellen i faser mellem dem vil knap kunne mærkes. termens amplitude og vil være større end termens amplitude.

På samme måde kan du reducere faseforskydningen og endda helt reducere den til nul, hvis du reducerer frekvensen af ​​generatoren på en eller anden måde. Et fald i frekvensen vil resultere i et fald i selvinduktions-EMK og derfor et fald i faseforskydningen mellem strømmen og spændingen i kredsløbet forårsaget af det.

Effekten af ​​et AC-kredsløb, der indeholder en induktor

Vekselstrømskredsløbet, der indeholder spolen, forbruger ikke strømkildens energi, og at der i kredsløbet er en energiudvekslingsproces mellem generatoren og kredsløbet.

Lad os nu analysere, hvordan tingene vil være med den strøm, der forbruges af en sådan ordning.

Strømforbruget i et AC-kredsløb er lig med produktet af strøm og spænding, men da strøm og spænding er variable størrelser, så vil effekten også være variabel.I dette tilfælde kan vi bestemme effektværdien for hvert tidspunkt i tiden, hvis vi multiplicerer den aktuelle værdi med den spændingsværdi, der svarer til et givet tidspunkt.

For at få effektgrafen skal vi gange værdierne af de lige linjesegmenter, der definerer strømmen og spændingen på forskellige tidspunkter. En sådan konstruktion er vist i fig. 3, a. Den stiplede bølgeform p viser os, hvordan effekten ændres i et AC-kredsløb, der kun indeholder induktiv modstand.

Følgende algebraiske multiplikationsregel blev brugt til at konstruere denne kurve: Når en positiv værdi ganges med en negativ værdi, opnås en negativ værdi, og når to negative eller to positive værdier ganges, opnås en positiv værdi.

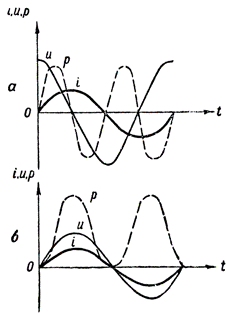
Figur 3. Effektgrafer: a — i et kredsløb, der indeholder induktiv modstand, b — også aktiv modstand

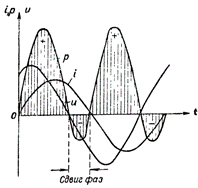
Figur 4. Effektplot for et kredsløb, der indeholder R og L.

Effektkurven ligger i dette tilfælde over tidsaksen. Det betyder, at der ikke er nogen energiudveksling mellem generatoren og kredsløbet, og derfor forbruges den strøm, som generatoren tilfører kredsløbet, fuldstændigt af kredsløbet.

I fig. 4 viser effektdiagrammet for et kredsløb indeholdende både induktiv og aktiv modstand. I dette tilfælde forekommer også den omvendte overførsel af energi fra kredsløbet til strømkilden, men i meget mindre grad end i et kredsløb med en enkelt induktiv modstand.

Efter at have gennemgået ovenstående effektgrafer konkluderer vi, at kun faseforskydningen mellem strøm og spænding i kredsløbet skaber "negativ" effekt.I dette tilfælde, jo større faseforskydning mellem strømmen og spænding i kredsløbet, jo mindre strøm vil kredsløbet forbruge, og omvendt, jo mindre faseforskydning, jo større effekt forbruges af kredsløbet.

Læs også: Hvad er spændingsresonans