Princippet om drift og enheden af ​​en enfaset transformer

Enfaset tomgangstransformer

Transformatorer i elektroteknik kaldes sådanne elektriske enheder, hvor vekselstrøm elektrisk energi fra en fast ledningsspole overføres til en anden fast ledningsspole, der ikke er elektrisk forbundet til den første.

Linket, der overfører energi fra den ene spole til den anden, er den magnetiske flux, som griber ind i de to spoler og ændrer sig konstant i størrelse og retning.

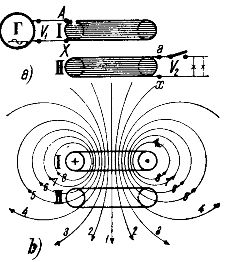
Ris. 1.

I fig. 1a viser den enkleste transformer bestående af to viklinger / og / / anbragt koaksialt over hinanden. Til spolen / leveres vekselstrøm fra generator D. Denne vikling kaldes primærvikling eller primærvikling. Med en vikling // kaldet en sekundær vikling eller sekundær vikling, er et kredsløb forbundet gennem modtagere af elektrisk energi.

Princippet for drift af transformeren

Transformatorens handling er som følger. Når der løber strøm i primærviklingen / skabes den magnetfelt, hvis kraftlinjer trænger ikke kun ind i viklingen, der skabte dem, men også delvist ind i sekundærviklingen //. Et omtrentligt billede af fordelingen af ​​kraftlinjerne skabt af primærviklingen er vist i fig. 1b.

Som det ses af figuren, er alle kraftlinjerne lukket rundt om spolens ledere /, men nogle af dem i fig. 1b er de elektriske ledninger 1, 2, 3, 4 også lukket omkring spolens ledninger //. Således er spole // magnetisk koblet til spole / ved hjælp af magnetiske feltlinjer.

Graden af ​​magnetisk kobling af spolerne / og //, med deres koaksiale arrangement, afhænger af afstanden mellem dem: jo længere spolerne er fra hinanden, jo mindre magnetisk kobling mellem dem, fordi jo færre kraftlinjer på coil /stick til spolen //.

Da spolen / passerer igennem, som vi antager, enfaset vekselstrøm, altså en strøm, der ændrer sig over tid efter en eller anden lov, for eksempel ifølge sinusloven, så vil det magnetiske felt, der skabes af den, også ændre sig over tid efter samme lov.

For eksempel, når strømmen i spolen / passerer gennem den største værdi, så passerer den magnetiske flux, der genereres af den, også gennem den største værdi; når strømmen i spolen / passerer gennem nul, ændrer dens retning, så passerer den magnetiske flux også gennem nul, og ændrer også retning.

Som et resultat af ændring af strømmen i spolen / bliver både spoler / og // gennemtrængt af en magnetisk flux, der konstant ændrer dens værdi og retning. Ifølge den grundlæggende lov om elektromagnetisk induktion induceres en vekselstrøm i spolen for hver ændring i den magnetiske flux, der trænger ind i spolen Elektromotorisk kraft… I vores tilfælde induceres den elektromotoriske kraft af selvinduktion i spolen /, og den elektromotoriske kraft af gensidig induktion induceres i spolen //.

Hvis enderne af spolen // er forbundet med et kredsløb af modtagere af elektrisk energi (se fig. 1a), så vil en strøm fremkomme i dette kredsløb; derfor modtager modtagerne elektrisk strøm. Samtidig vil energi blive rettet til viklingen /fra generatoren, næsten lig med den energi, der gives til kredsløbet af viklingen //. På denne måde vil elektrisk energi fra den ene spole blive overført til den anden spoles kredsløb, som galvanisk (metallisk) er fuldstændig uafhængig af den første spole.I dette tilfælde er midlet til energitransmission kun en vekslende magnetisk flux.

Vist i fig. 1a er transformeren meget ufuldkommen, fordi der er ringe magnetisk kobling mellem primærviklingen /og sekundærviklingen //.

Den magnetiske kobling af to spoler estimeres generelt ved forholdet mellem den magnetiske flux koblet til de to spoler og fluxen skabt af en spole.

Fig. 1b kan det ses, at kun en del af spolens feltlinjer /er lukket omkring spolen //. Den anden del af elledningerne (i fig. 1b — linjerne 6, 7, 8) er kun lukket omkring spolen /. Disse elledninger er slet ikke involveret i overførslen af ​​elektrisk energi fra den første spole til den anden, de danner det såkaldte herrefelt.

For at øge den magnetiske kobling mellem de primære og sekundære viklinger og samtidig reducere den magnetiske modstand for passage af den magnetiske flux, placeres viklingerne af tekniske transformere på helt lukkede jernkerner.

Det første eksempel på implementering af transformere er vist skematisk i fig. 2 enfaset transformer af den såkaldte stangtype. Dens primære og sekundære spoler c1 og c2 er placeret på jernstænger a — a, forbundet i enderne med jernplader b — b, kaldet åg. På denne måde danner to stænger a, a og to åg b, b en lukket jernring, hvori den magnetiske flux passerer blokeret med de primære og sekundære viklinger. Denne jernring kaldes transformatorens kerne.

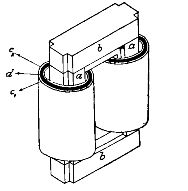Ris. 2.

Den anden udførelsesform for transformere er vist skematisk i fig. 3 enfaset transformer af den såkaldte pansrede type. I denne transformer er de primære og sekundære viklinger c, der hver består af en række flade viklinger, placeret på en kerne dannet af to stænger af to jernringe a og b. Ringene a og b, der omgiver viklingerne, dækker dem næsten udelukkende med panser, derfor kaldes den beskrevne transformer panser. Den magnetiske flux, der passerer inde i spolerne c, er opdelt i to lige store dele, som hver er indesluttet i sin egen jernring.

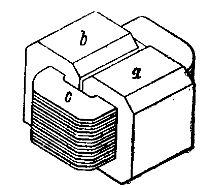
Ris. 3

Brugen af ​​lukkede jernmagnetiske kredsløb i transformere opnår en betydelig reduktion i lækstrøm. I sådanne transformere er fluxene forbundet med de primære og sekundære viklinger næsten lig med hinanden. Hvis vi antager, at de primære og sekundære viklinger er gennemtrængt af den samme magnetiske flux, kan vi skrive udtryk baseret på det totale inducerede stød for de øjeblikkelige værdier af viklingernes elektromotoriske kræfter:

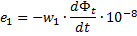
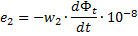
I disse udtryk, w1 og w2 - antallet af vindinger af de primære og sekundære viklinger, og dFt er størrelsen af ​​ændringen i den gennemtrængende vikling af den magnetiske flux pr. tidselement dt, derfor er der en ændringshastighed af den magnetiske flux . Fra de sidste udtryk kan følgende relation fås:

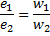
dvs. angivet i de primære og sekundære viklinger / og // er de momentane elektromotoriske kræfter relateret til hinanden på samme måde som antallet af vindinger af spolerne. Den sidste konklusion er gyldig ikke kun med hensyn til de øjeblikkelige værdier af elektromotoriske kræfter, men også med hensyn til deres største og effektive værdier.

Den elektromotoriske kraft induceret i primærviklingen, som en elektromotorisk kraft af selvinduktion, balancerer næsten fuldstændigt spændingen påført den samme vikling... Hvis du med E1 og U1 angiver de effektive værdier for den elektromotoriske kraft af primærviklingen og spændingen på den, så kan du skrive:

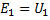
Den elektromotoriske kraft, der induceres i sekundærviklingen, er i det pågældende tilfælde lig med spændingen over enderne af denne vikling.

Hvis du, som den foregående, gennem E2 og U2 angiver de effektive værdier af sekundærviklingens elektromotoriske kraft og spændingen ved dens ender, så kan du skrive:

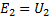
Derfor kan du ved at påføre en spænding på den ene vikling af transformeren få en hvilken som helst spænding i enderne af den anden spole, du skal blot tage et passende forhold mellem antallet af vindinger af disse spoler. Dette er hvad transformatorens hovedegenskab er.

Forholdet mellem antallet af vindinger af primærviklingen og antallet af vindinger af sekundærviklingen kaldes transformatorens transformationsforhold... Vi vil betegne transformationskoefficienten kT.

Derfor kan man skrive:

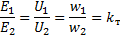
En transformer, hvis transformationsforhold er mindre end én, kaldes en step-up transformer, fordi spændingen i sekundærviklingen, eller den såkaldte sekundære spænding, er større end spændingen i primærviklingen, eller den såkaldte primærspænding . En transformer med et transformationsforhold større end én kaldes en step-down transformer, da dens sekundære spænding er mindre end den primære.

Drift af en enfaset transformer under belastning

Under tomgang af transformeren skabes den magnetiske flux af den primære viklingsstrøm eller rettere af den magnetomotoriske kraft af den primære vikling. Da transformatorens magnetiske kredsløb er lavet af jern og derfor har en lav magnetisk modstand, og antallet af vindinger af primærviklingen generelt antages at være stort, er transformatorens tomgangsstrøm lille, den er 5- 10 % af normalen.

Hvis du lukker den sekundære spole til en vis modstand, så vil den magnetomotoriske kraft af denne spole også fremkomme med forekomsten af ​​strøm i den sekundære spole.

Ifølge Lenz's lov virker den magnetomotoriske kraft af den sekundære spole mod den magnetomotoriske kraft af den primære spole

Det ser ud til, at den magnetiske flux i dette tilfælde skal falde, men hvis en konstant spænding påføres primærviklingen, vil der næsten ikke være noget fald i magnetisk flux.

Faktisk er den elektromotoriske kraft, der induceres i primærviklingen, når transformatoren belastes, næsten lig med den påførte spænding. Denne elektromotoriske kraft er proportional med den magnetiske flux.Derfor, hvis den primære spænding er konstant i størrelse, skal den elektromotoriske kraft under belastning forblive næsten den samme, som den var under tomgangsdrift af transformeren. Denne omstændighed fører til næsten fuldstændig konstanthed af den magnetiske flux under enhver belastning.

Ved en konstant værdi af primærspændingen ændres transformatorens magnetiske flux næppe med belastningsændringen og kan antages lig med den magnetiske flux under tomgangsdrift.

Transformatorens magnetiske flux kan kun opretholde sin værdi under belastning, fordi når der opstår en strøm i sekundærviklingen, øges strømmen i primærviklingen også, så meget at forskellen mellem de magnetomotoriske kræfter eller ampere-omdrejninger i primær- og sekundærviklingen viklinger forbliver næsten lig med den magnetomotoriske kraft eller ampere-drejninger under tomgang ... Således er udseendet af en afmagnetiserende magnetomotorisk kraft eller ampere-drejninger i sekundærviklingen ledsaget af en automatisk stigning i den magnetomotoriske kraft af den primære vikling.

Da der som nævnt ovenfor kræves en lille magnetomotorisk kraft for at skabe en transformatormagnetisk flux, kan man sige, at en stigning i den sekundære magnetomotoriske kraft er ledsaget af en stigning i den primære magnetomotoriske kraft, som er næsten den samme i størrelse.

Derfor kan man skrive:

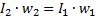
Fra denne lighed opnås transformatorens anden hovedkarakteristik, nemlig forholdet:

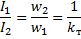
hvor kt er transformationsfaktoren.

Derfor er forholdet mellem strømmene af transformatorens primære og sekundære viklinger lig med en divideret med transformationsforholdet.

Så, transformatorens vigtigste egenskaber have et forhold

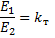
og

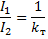
Hvis vi multiplicerer venstre side af forholdet med hinanden og højre sider med hinanden, får vi

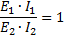
og

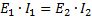
Den sidste lighed giver transformatorens tredje karakteristik, som kan udtrykkes med ord som dette: den effekt, der leveres af transformatorens sekundære vikling i volt-ampere, er næsten lig med den effekt, der leveres til primærviklingen også i volt-ampere .

Hvis vi ignorerer energitabene i viklingernes kobber og i transformatorkernens jern, kan vi sige, at al den strøm, der leveres til transformatorens primære vikling fra strømkilden, overføres til dens sekundære vikling, og senderen er den magnetiske flux.