Hvad er spændingstab og årsagerne til spændingstab

Tab af netspænding

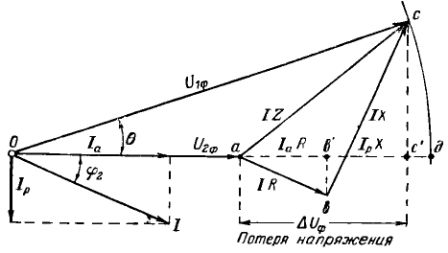
For at forstå, hvad spændingstab er, skal du overveje spændingsvektordiagrammet for en trefaset AC-ledning (fig. 1) med en enkelt belastning for enden af ​​linjen (fig. 1)I).

Antag, at den aktuelle vektor er dekomponeret i komponenterne Azi og AzP. I fig. 2 er fasespændingsvektorerne for enden af ​​linjen tegnet i skala U3ph og strøm AziLing i fase med en vinkel φ2.

For at få spændingsvektoren i begyndelsen af ​​linjen U1φ følger vektoren i slutningen U2ph, tegnes spændingsfaldstrekanten (abc) på spændingsskalaen. Til dette er vektoren ab, lig med produktet af strøm og aktiv modstand af linjen (AzR), placeret parallelt med strømmen, og vektoren b° C, lig med produktet af strøm og induktiv modstand af linjen ( AzX), er vinkelret på den aktuelle vektor .Under disse forhold svarer den lige linje, der forbinder punkterne O og c, til størrelsen og positionen i rummet af spændingsvektoren ved begyndelsen af ​​linjen (U1e) i forhold til spændingsvektoren i slutningen af ​​linjen (U2e). Ved at forbinde enderne af vektorerne U1f og U2e får vi spændingsfaldsvektoren for den lineære impedans ac = IZ.

Ris. 1. Skematisk med en enkelt end-of-line belastning

Ris. 2. Vektordiagram over spændinger for en linje med en enkelt belastning. Tab af netspænding.

Aftal at kalde spændingstab den algebraiske forskel mellem fasespændingerne i begyndelsen og slutningen af ​​linjen, det vil sige segment ad eller næsten lige segment ac '.

Vektordiagrammet og relationerne afledt af det viser, at spændingstabet afhænger af netværkets parametre såvel som af de aktive og reaktive komponenter af strømmen eller belastningen.

Ved beregning af størrelsen af ​​spændingstab i netværket skal der altid tages hensyn til den aktive modstand, og den induktive modstand kan negligeres i lysnetværk og i netværk udført med tværsnit op til 6 mm2 og kabler op til 35 mm2.

Bestemmelse af spændingstab i netværket

Spændingstabet for et trefaset system er normalt angivet for lineære størrelser, som bestemmes af formlen

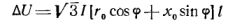
hvor l — længden af ​​den tilsvarende sektion af nettet, km.

Hvis vi erstatter strøm med effekt, vil formlen have formen:

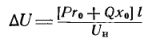
hvor P. — aktiv effekt, B- reaktiv effekt, kVar; l — strækningens længde, km; Un — nominel netværksspænding, kV.

Ændring i netspænding

Tilladt spændingsfald

For hver strømmodtager et vist spændingstab... For eksempel har induktionsmotorer en spændingstolerance på ± 5 % under normale forhold.Dette betyder, at hvis den nominelle spænding for denne elektriske motor er 380 V, så skal spændingen U„extra = 1,05 Un = 380 x1,05 = 399 V og U»add = 0,95 Un = 380 x 0,95 = 361 V betragtes som de maksimalt tilladte spændingsværdier. Naturligvis vil alle mellemspændinger mellem værdierne 361 og 399 V også tilfredsstille brugeren og udgøre en bestemt zone, der kan kaldes zonen med ønskede spændinger.

Da der under driften af ​​virksomheden er en konstant ændring i belastningen (strøm eller strøm strømmer gennem ledningerne på et bestemt tidspunkt af dagen), vil der forekomme forskellige spændingstab i netværket, varierende fra de højeste tilsvarende værdier til den maksimale belastningstilstand dUmax, til den mindste dUmin svarende til brugerens minimumsbelastning.

For at beregne størrelsen af ​​disse spændingstab skal du bruge formlen:

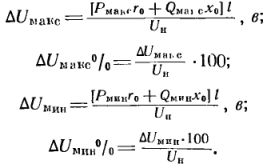
Af vektordiagrammet over spændinger (fig. 2) følger, at den faktiske spænding for modtageren U2f kan opnås, hvis vi trækker værdien dUf fra spændingen i begyndelsen af ​​linjen U1f, eller skifter til en lineær, dvs. fase -til-fase spænding, får vi U2 = U1 — dU

Beregning af spændingstab

Et eksempel. Forbrugeren, der består af asynkrone motorer, er forbundet til busserne i virksomhedens transformatorstation, som opretholder en konstant spænding hele dagen U1 = 400 V.

Den højeste brugerbelastning noteres kl. 11, mens spændingstabet dUmax = 57 V, eller dUmax% = 15%. Den mindste forbrugsbelastning svarer til frokostpausen, mens dUmin — 15,2 V, eller dUmin% = 4%.

Det er nødvendigt at bestemme den faktiske spænding hos brugeren i højeste og laveste belastningstilstand og kontrollere, at den er inden for det ønskede spændingsområde.

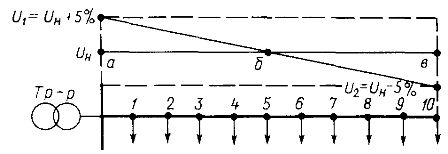
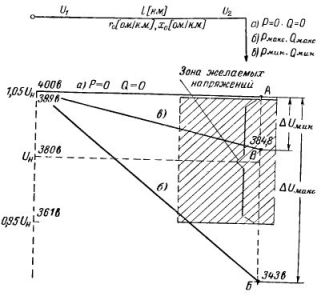Ris. 3. Potentialediagram for en linje med en enkelt belastning til bestemmelse af spændingstabet

Svar. Bestem de faktiske spændingsværdier:

U2Max = U1 — dUmax = 400 — 57 = 343 V

U2min = U1 — dUmin = 400 — 15,2 = 384,8V

Den ønskede spænding for asynkronmotorer med Un = 380 V skal opfylde betingelsen:

399 ≥ U2zhel ≥ 361

Ved at erstatte de beregnede spændingsværdier med uligheden sikrer vi, at for den største belastningstilstand er forholdet 399> 343> 361 ikke opfyldt, og for de mindste belastninger er 399> 384,8> 361 opfyldt.

Afslut. I tilstanden med største belastninger er spændingstabet så stort, at spændingen hos brugeren går ud af zonen med de ønskede spændinger (fald) og ikke tilfredsstiller brugeren.

Dette eksempel kan illustreres grafisk ved potentialediagrammet i fig. 3. I mangel af strøm vil spændingen hos brugeren være numerisk lig spændingen på forsyningsbusserne. Da spændingsfaldet er proportionalt med forsyningsledningens længde, ændres spændingen ved tilstedeværelse af en belastning langs linjen i en skrånende lige linje fra værdien U1 = 400 V til værdien U2Max = 343 V og U2min = 384,8 V .

Som det fremgår af diagrammet, har spændingen ved højeste belastning forladt zonen med ønskede spændinger (punkt B på grafen).

Selv med en konstant spænding på forsyningstransformatorskinnerne kan pludselige ændringer i belastningen således skabe en uacceptabel spændingsværdi ved modtageren.

Derudover kan det ske, at når belastningen på netværket skifter fra den højeste belastning om dagen til den laveste belastning om natten, vil elsystemet ikke selv være i stand til at levere den nødvendige spænding ved transformatorterminalerne. I begge tilfælde skal man ty til lokal, hovedsagelig spændingsændring.

Tab af spænding i transformeren (på billeder)