Resonans af strømme

Parallelforbindelse af en kondensator og en induktor i et vekselstrømskredsløb

Overvej fænomenerne i kæden vekselstrømindeholdende en generator, kondensator og induktor forbundet parallelt. Antag, at kredsløbet ikke har nogen aktiv modstand.

Det er klart, at i et sådant kredsløb er spændingen af ​​både spolen og kondensatoren til enhver tid lig med spændingen udviklet af generatoren.

Den samlede strøm i et kredsløb består af strømmene i dets grene. Strømmen i den induktive gren forsinker spændingen i fase med en fjerdedel af perioden, og strømmen i den kapacitive gren fører den med samme fjerdedel af perioden. Derfor viser strømmene i grenene sig på et hvilket som helst tidspunkt at være faseforskudt i forhold til hinanden med en halv periode, det vil sige, at de er i modfase. Således er strømmene i grenene til enhver tid rettet mod hinanden, og den samlede strøm i den uforgrenede del af kredsløbet er lig med deres forskel.

Dette giver os ret til at skrive lighed I = IL -integral kredsløb

hvor jeg- effektive værdi af den samlede strøm i kredsløbet, I L og integreret kredsløb — effektive værdier af strømme i grenene.

Ved at bruge Ohms lov til at bestemme de effektive værdier af strømmen i grenene får vi:

Il = U/XL og Az°C = U/XC

Hvis kredsløbet er domineret af induktiv modstand, dvs. XL Mere ▼ XC, strømmen i spolen er mindre end strømmen i kondensatoren; derfor er strømmen i den uforgrenede del af kredsløbet kapacitiv af natur, og kredsløbet som helhed for generatoren vil være kapacitivt. Omvendt, med XC større end XL, er strømmen i kondensatoren mindre end strømmen i spolen; derfor er strømmen i den uforgrenede del af kredsløbet induktiv, og kredsløbet som helhed for generatoren vil være induktivt.

Det skal ikke glemmes, at belastningen i begge tilfælde er reaktiv, dvs. kredsløbet bruger ikke generatorens strøm.

Resonans af strømme

Lad os nu overveje det tilfælde, hvor kondensatoren og spolen forbundet parallelt viste sig at være ens i deres reaktans, dvs. XlL = X°C.

Hvis vi som før antager, at spolen og kondensatoren ikke har nogen aktiv modstand, så hvis deres reaktioner er ens (YL = Y° C), vil den samlede strøm i den uforgrenede del af kredsløbet være nul, mens i grenene er lig med strømme vil flyde med størst størrelse. I dette tilfælde forekommer fænomenet resonansstrømme i kredsløbet.

Ved strømresonans vil de effektive værdier af strømmene i hver gren, bestemt af forholdene IL = U / XL og Аz° С = U / XC, være lig med hinanden, således at XL = XC.

Den konklusion, vi nåede frem til, kan ved første øjekast virke ret underlig. Faktisk er generatoren belastet med to modstande, og der er ingen strøm i den uforgrenede del af kredsløbet, mens der løber lige store og i øvrigt de største strømme i selve modstandene.

Dette forklares af opførselen af ​​spolens magnetfelt og elektrisk felt af en kondensator… Ved resonans af strømme, som i spændingsresonans, er der en energiudsving mellem spolens felt og kondensatorens felt. Generatoren, efter at have kommunikeret energien til kredsløbet, ser ud til at være isoleret. Den kan slukkes helt, og strømmen i den forgrenede del af kredsløbet vil blive opretholdt uden en generator af den energi, som kredsløbet i første omgang lagrer. Spændingen over kredsløbsterminalerne vil også forblive nøjagtig den samme som den, der udvikles af generatoren.

Når induktoren og kondensatoren er forbundet parallelt, opnåede vi således et oscillatorkredsløb, der kun adskiller sig fra det ovenfor beskrevne ved, at generatoren, der skaber svingningerne, ikke er forbundet direkte med kredsløbet, og kredsløbet er lukket. 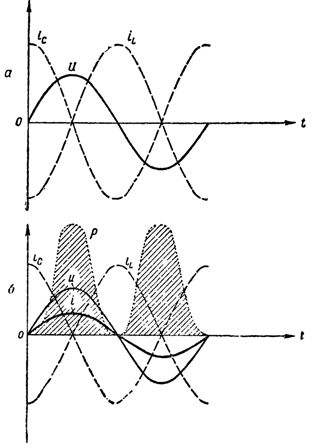Grafer over strømme, spænding og effekt i kredsløbet ved resonans af strømme: a — den aktive modstand er lig nul, kredsløbet forbruger ikke energi; b — kredsløbet har en aktiv modstand, en strøm er opstået i den uforgrenede del af kredsløbet, kredsløbet bruger energi

L, C og e, hvor der opstår strømresonans, bestemmes, som i spændingsresonans (hvis vi forsømmer kredsløbets aktive modstand), af ligheden:

ωL = 1 / ω° C

Derfor:

eres = 1 / 2π√LC

Lres = 1 / ω2C

Stykke = 1 / ω2L

Ved at ændre en hvilken som helst af disse tre størrelser, kan ligheden Xl = X° C opnås, dvs. omdanne kredsløbet til et oscillerende kredsløb.

Så vi har et lukket oscillerende kredsløb, hvor vi kan inducere elektriske svingninger, dvs. vekselstrøm. Og hvis det ikke var for den aktive modstand, som ethvert oscillerende kredsløb besidder, kunne der konstant eksistere en vekselstrøm i det.Tilstedeværelsen af ​​aktiv modstand fører til, at svingningerne i kredsløbet gradvist dør ned, og for at opretholde dem er der brug for en energikilde - en generator.

I ikke-sinusformede strømkredsløb er resonanstilstande mulige for forskellige harmoniske komponenter.

Resonansstrømme er meget udbredt i praksis. Fænomenet strømresonans bruges i båndpasfiltre som en elektrisk "klemme", der forsinker en bestemt frekvens. Da der er en betydelig strømmodstand ved frekvens f, vil spændingsfaldet i kredsløbet ved frekvens f være maksimalt. Denne egenskab ved sløjfen kaldes selektivitet, den bruges i radiomodtagere til at isolere signalet fra en bestemt radiostation. Et oscillerende kredsløb, der fungerer i en resonanstilstand af strømme, er en af ​​hovedkomponenterne elektroniske generatorer.