Hvad er en elektrisk forsyning?

Det moderne menneske møder konstant elektricitet i hverdagen og på arbejdet, bruger enheder, der forbruger elektrisk strøm, og enheder, der genererer den. Når du arbejder med dem, bør du altid tage hensyn til deres evner, der er iboende i de tekniske egenskaber.

En af hovedindikatorerne for enhver elektrisk enhed er sådan en fysisk størrelse som elektrisk energi... Det er sædvanligt at kalde intensiteten eller hastigheden af ​​generering, transmission eller omdannelse af elektricitet til andre typer energi, for eksempel varme, lys, mekanisk.

Transport eller overførsel af stor elektrisk energi til industrielle formål udføres iht højspændingsledninger.

Transformation elektrisk energi udføres på transformerstationer.

Elforbrug forekommer i husholdnings- og industriapparater til forskellige formål. En af deres almindelige typer er glødelamper af forskellige klassifikationer.

Den elektriske effekt fra generatorer, elledninger og forbrugere i DC- og AC-kredsløb har samme fysiske betydning, som samtidig udtrykkes i forskellige forhold afhængigt af formen af ​​de sammensatte signaler. For at definere de generelle mønstre, forestillinger om øjeblikkelige værdier... De understreger igen afhængigheden af ​​hastigheden af ​​transformation af elektricitet til tiden.

Bestemmelse af øjeblikkelig elektrisk effekt

I teoretisk elektroteknik bruges deres billeder i form af øjeblikkelige værdier, som er fastsat på et bestemt tidspunkt, for at udlede de grundlæggende forhold mellem strøm, spænding og effekt.

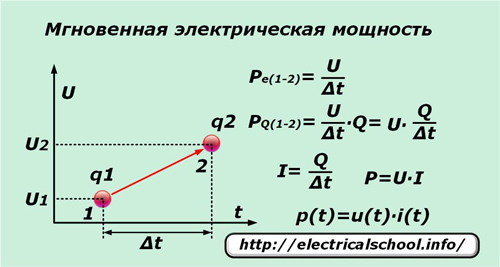
Hvis en enkelt elementær ladning q på meget kort tid ∆t under påvirkning af spænding U bevæger sig fra punkt «1» til punkt «2», så udfører den arbejde svarende til potentialforskellen mellem disse punkter. Ved at dividere det med tidsintervallet ∆t får vi udtrykket for den øjeblikkelige effekt pr. ladningsenhed Pe (1-2).

Da ikke kun den enkelte ladning bevæger sig under påvirkning af den påførte spænding, men også alle de tilstødende, der er under indflydelse af denne kraft, hvis antal er bekvemt repræsenteret af tallet Q, så er den øjeblikkelige værdi af effekten PQ (1-2) kan skrives til dem.

Efter at have udført simple transformationer får vi udtrykket for effekten P og afhængigheden af ​​dens øjeblikkelige værdi p (t) af komponenterne i produktet af den øjeblikkelige strøm i (t) og spændingen u (t).

Bestemmelse af konstant elektrisk effekt

V DC kredsløb størrelsen af ​​spændingsfaldet i kredsløbssektionen og strømmen, der strømmer gennem den, ændres ikke og forbliver stabil, lig med de øjeblikkelige værdier.Derfor kan effekten i dette kredsløb bestemmes ved at multiplicere disse værdier eller dividere det perfekte arbejde A med perioden for dets udførelse, som vist på det forklarende billede.

Bestemmelse af elektrisk vekselstrøm

Lovene om sinusformet variation af strømme og spændinger, der transmitteres gennem elektriske netværk, pålægger deres indflydelse på udtryk for effekt i sådanne kredsløb. Her spiller tilsyneladende kraft ind, som beskrives af potenstrekanten og består af aktive og reaktive komponenter.

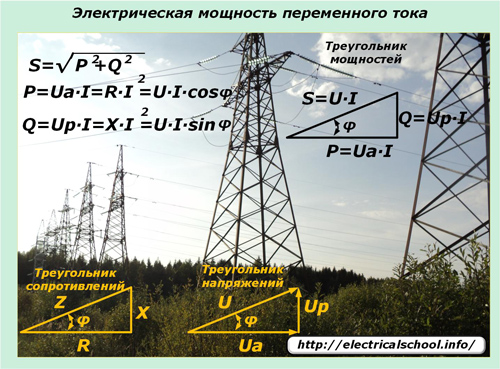
En sinusformet elektrisk strøm, når den passerer gennem elledninger med blandede typer belastninger i alle sektioner, ændrer ikke formen på dens harmoniske. Og spændingsfaldet ved reaktive belastninger skifter i fase i en bestemt retning. Momentværdiudtryk hjælper med at forstå effekten af ​​påførte belastninger på effektændringen i kredsløbet og dets retning.

Samtidig skal du straks være opmærksom på, at retningen af ​​strømstrømmen fra generatoren til forbrugeren og den transmitterede effekt gennem det oprettede kredsløb er helt forskellige ting, som i nogle tilfælde ikke kun kan falde sammen, men også være rettet i modsatte retninger.

Overvej disse forhold i deres ideelle, rene manifestation for forskellige typer belastninger:

• aktiv;

• kapacitiv;

• induktiv.

Aktiv belastningseffekttab

Vi vil antage, at generatoren producerer en ideel sinusformet spænding u, som påføres kredsløbets rent aktive modstand. Amperemeter A og voltmeter V måler strøm I og spænding U hver gang t.

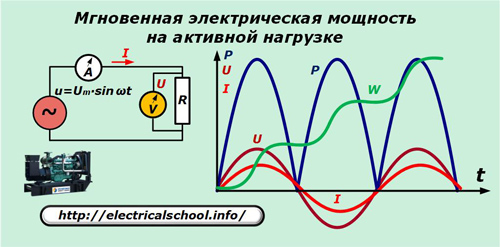
Grafen viser, at strømmens sinusoider og spændingsfaldet over den aktive modstand matcher i frekvens og fase, hvilket giver de samme svingninger. Kraften udtrykt af deres produkt oscillerer med dobbelt frekvens og forbliver altid positiv.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Hvis vi går til udtrykket driftsspænding, så får vi: p = P ∙ (1-cos2ωt).

Vi vil så integrere effekten over perioden af ​​en svingning T, og vi vil kunne bemærke, at energiforstærkningen ∆W i løbet af dette interval stiger. Over tid fortsætter modstanden med at forbruge nye portioner elektricitet, som vist på grafen.

Med reaktive belastninger er egenskaberne ved energiforbrug forskellige, de har en anden form.

Kapacitiv effekttab

I generatorens elektriske kredsløb skal du udskifte det resistive element med en kondensator med kapacitans C.

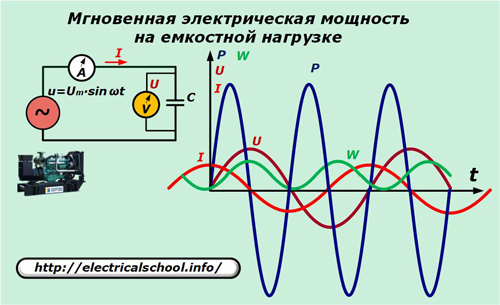
Forholdet mellem strømmen og spændingsfaldet i kapacitansen er udtrykt ved forholdet: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Vi multiplicerer værdierne af de øjeblikkelige udtryk for strøm med spænding og får værdien af ​​den effekt, der forbruges af den kapacitive belastning.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt sin = U2) ωt.

Her kan du se, at effekten svinger omkring nul ved dobbelt frekvens af den påførte spænding. Dens samlede værdi for den harmoniske periode, såvel som energiforstærkningen, er nul.

Det betyder, at energi bevæger sig langs kredsløbets lukkede kredsløb i begge retninger, men ikke virker.En sådan kendsgerning forklares ved, at når kildespændingen stiger i absolut værdi, er effekten positiv, og energistrømmen gennem kredsløbet ledes til beholderen, hvor energi akkumuleres.

Efter at spændingen passerer til den faldende harmoniske sektion, returneres energi fra kondensatoren til kredsløbet til kilden. Intet nyttigt arbejde udføres i nogen af ​​processerne.

Effekttab i en induktiv belastning

Udskift nu kondensatoren i forsyningskredsløbet med induktans L.

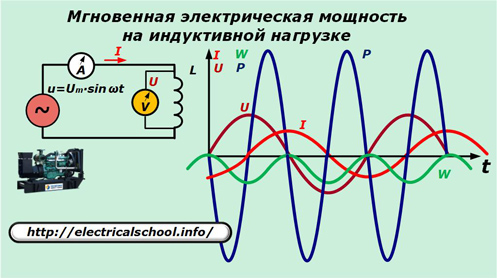
Her er strømmen gennem induktansen udtrykt ved forholdet:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Så får vi

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sinω2ωt (2ХL) ∙ t sinω2ωt (2).

De resulterende udtryk giver os mulighed for at se arten af ​​ændringen i kraftens retning og stigningen af ​​energi på induktansen, som udfører de samme svingninger, der er ubrugelige til at udføre arbejde, som på kapacitansen.

Den effekt, der frigives i reaktive belastninger, kaldes reaktiv komponent. Under ideelle forhold, når forbindelsesledningerne ikke har nogen aktiv modstand, virker det harmløst og forårsager ingen skade. Men under reelle strømforhold forårsager periodiske transienter og udsving i reaktiv effekt opvarmning af alle aktive elementer, inklusive forbindelsesledninger, for hvilke der forbruges noget energi, og værdien af ​​den anvendte fulde effekt af kilden falder.

Den største forskel mellem den reaktive komponent af strøm er, at den slet ikke udfører nyttigt arbejde, men fører til tab af elektrisk energi og overskydende belastninger på udstyr, som er særligt farlige i kritiske situationer.

Af disse grunde, for at eliminere indflydelsen af ​​reaktiv effekt, f.eks tekniske systemer til kompensation.

Strømfordeling ved blandet belastning

Som et eksempel bruger vi belastningen af ​​en generator med en aktiv kapacitiv karakteristik.

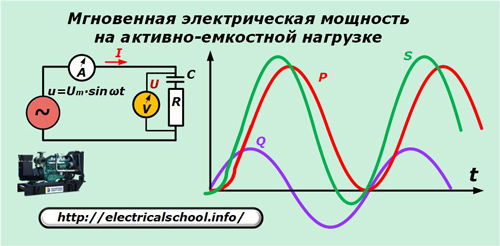
For at forenkle billedet er sinusoiderne af strømme og spændinger ikke vist i den givne graf, men det skal huskes, at med en aktiv-kapacitiv karakter af belastningen, fører strømvektoren spændingen.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Efter transformationer får vi: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Disse to udtryk i det sidste udtryk er de aktive og reaktive komponenter af den øjeblikkelige tilsyneladende kraft. Kun den første af disse virker nyttigt.

Værktøjer til effektmåling

For at analysere forbruget af elektricitet og beregne for det, bruges måleapparater, som længe har været kaldt "Tællere"… Deres arbejde er baseret på at måle de effektive værdier af strøm og spænding og automatisk multiplicere dem med et output af information.

Målere viser energiforbruget ved at tælle elektriske apparaters driftstid på en trinvis basis fra det øjeblik, måleren tændes under belastning.

For at måle den aktive komponent af strøm i AC-kredsløb, wattmålere, og reaktive - varmetere. De har forskellige enhedsbetegnelser:

• watt (W, W);

• var (var, var, var).

For at bestemme det samlede energiforbrug er det nødvendigt at beregne dens værdi ved hjælp af krafttrekantformlen baseret på aflæsningerne af wattmeteret og varmeteret. Det udtrykkes i sine egne enheder - volt-ampere.

De accepterede betegnelser for hver enheds enhed hjælper elektrikere med at bedømme ikke kun dens værdi, men også arten af ​​strømkomponenten.