Elektrisk modstand af ledninger
Begrebet elektrisk modstand og ledningsevne
Ethvert legeme, hvorigennem en elektrisk strøm løber, har en vis modstand mod det. Egenskaben ved et ledende materiale til at forhindre en elektrisk strøm i at passere gennem det kaldes elektrisk modstand.
Elektronisk teori forklarer arten af den elektriske modstand af metalliske ledere på denne måde. Frie elektroner, når de bevæger sig langs en ledning, møder atomer og andre elektroner på deres vej utallige gange og mister uundgåeligt noget af deres energi, når de interagerer med dem. Elektroner oplever alligevel modstand mod deres bevægelse. Forskellige metalledere med forskellige atomare strukturer har forskellig modstand mod elektrisk strøm.
Præcis det samme forklarer væskelederes og gassers modstand mod passage af elektrisk strøm. Vi må dog ikke glemme, at i disse stoffer møder ikke elektroner, men ladede partikler af molekyler modstand under deres bevægelse.
Modstand er angivet med de latinske bogstaver R eller r.
Ohm tages som enheden for elektrisk modstand.
Ohm er modstanden af en kviksølvsøjle 106,3 cm høj med et tværsnit på 1 mm2 ved en temperatur på 0 °C.
Hvis for eksempel ledningens elektriske modstand er 4 ohm, så skrives det således: R = 4 ohm eller r = 4 th.
Til måling af modstande af stor værdi anvendes en enhed kaldet megohm.
En megohm er lig med en million ohm.
Jo større modstand ledningen er, jo dårligere leder den elektrisk strøm, og omvendt, jo lavere modstand ledningen er, jo lettere er det for elektrisk strøm at passere gennem denne ledning.
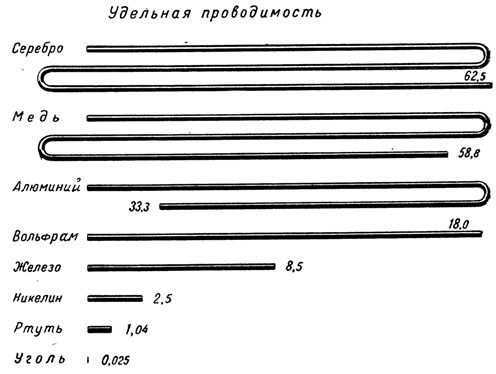
Derfor kan man for egenskaberne af en leder (fra synspunktet om passage af en elektrisk strøm gennem den) tage hensyn til ikke kun dens modstand, men også værdien omvendt af modstanden og kaldet ledningsevne.

Elektrisk ledningsevne kaldes et materiales evne til at føre en elektrisk strøm gennem sig selv.
Da konduktans er modstandens gensidige, udtrykkes den som 1 /R, konduktansen er betegnet med det latinske bogstav g.
Indflydelse af lederens materiale, dens dimensioner og omgivelsestemperaturen på værdien af elektrisk modstand
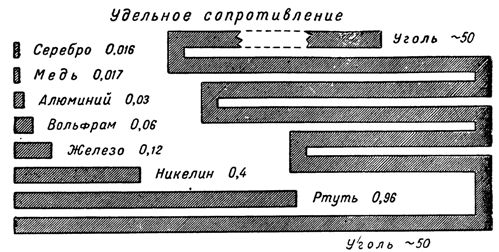
Modstanden af forskellige ledninger afhænger af det materiale, de er lavet af. For at karakterisere den elektriske modstand af forskellige materialer, begrebet den såkaldte Modstand.
 Modstand kaldes modstanden af en ledning med en længde på 1 m og et tværsnitsareal på 1 mm2. Modstand er betegnet med det græske bogstav r. Hvert materiale, som en leder er lavet af, har sin egen specifikke modstand.
Modstand kaldes modstanden af en ledning med en længde på 1 m og et tværsnitsareal på 1 mm2. Modstand er betegnet med det græske bogstav r. Hvert materiale, som en leder er lavet af, har sin egen specifikke modstand.
For eksempel er modstanden af kobber 0,017, det vil sige, en kobbertråd med en længde på 1 m og et tværsnit på 1 mm2 har en modstand på 0,017 ohm. Modstanden af aluminium er 0,03, modstanden af jern er 0,12, modstanden af konstantan er 0,48, og modstanden af nichrom er 1-1,1.
Læs mere om det her: Hvad er elektrisk modstand?
Modstanden af en ledning er direkte proportional med dens længde, det vil sige, jo længere ledningen er, jo større er dens elektriske modstand.
Modstanden af en ledning er omvendt proportional med dens tværsnitsareal, det vil sige, jo tykkere ledning, jo lavere modstand, og omvendt, jo tyndere ledning, jo højere modstand.
For bedre at forstå dette forhold, forestil dig to par kommunikerende kar, et par kar har et tyndt forbindelsesrør og det andet et tykt. Det er klart, at når et af karrene (hvert par) er fyldt med vand, vil dets overførsel til et andet kar gennem et tykt rør ske meget hurtigere end gennem et tyndt, dvs. et tykt rør vil have mindre modstand mod strømmen af vand. På samme måde er det lettere for en elektrisk strøm at passere gennem en tyk ledning end gennem en tynd, det vil sige, at førstnævnte har mindre modstand end sidstnævnte.
En leders elektriske modstand er lig med den specifikke modstand af det materiale, som denne leder er lavet af, ganget med længden af lederen og divideret med arealet af tværsnitsarealet af leder:
R = p l/S,
hvor — R — ledningens modstand, ohm, l — længden i ledningen i m, C — ledningens tværsnitsareal, mm2.
Tværsnitsareal af en rund ledning beregnet ved formlen:
S = Pi xd2 / 4
hvor Pi er en konstant værdi lig med 3,14; d — trådens diameter.
Og sådan bestemmes ledningens længde:
l = S R / p,
Denne formel gør det muligt at bestemme længden af ledningen, dens tværsnit og modstand, hvis de andre mængder, der er inkluderet i formlen, er kendte.
Hvis det er nødvendigt at bestemme ledningens tværsnitsareal, fører formlen til følgende form:
S = p l/R
Ved at transformere den samme formel og løse ligheden i form af p, finder vi ledningens modstand:
R = R S/l
Sidstnævnte formel skal bruges i tilfælde, hvor lederens modstand og dimensioner er kendt, men dens materiale er ukendt, og desuden er det vanskeligt at bestemme ud fra dens udseende. For at gøre dette er det nødvendigt at bestemme ledningens modstand og ved hjælp af tabellen finde et materiale med en sådan modstand.

En anden faktor, der påvirker modstanden af ledninger, er temperatur.
Det er blevet fastslået, at med en stigning i temperaturen øges modstanden af metaltråde, og med et fald falder den. Denne stigning eller fald i modstand for rene metalledere er næsten den samme og er i gennemsnit 0,4 % pr. 1 °C... Modstanden af væskeledere og kul falder med stigende temperatur.
 Den elektroniske teori om stofstrukturen giver følgende forklaring på stigningen i modstand af metalledere med stigende temperatur.Når den opvarmes, modtager lederen termisk energi, som uundgåeligt overføres til alle atomer af stoffet, som et resultat af, at intensiteten af deres bevægelse øges. Den øgede bevægelse af atomer skaber større modstand mod den rettede bevægelse af frie elektroner, hvorfor lederens modstand øges. Efterhånden som temperaturen falder, skabes der bedre betingelser for retningsbestemt bevægelse af elektroner, og lederens modstand falder. Dette forklarer et interessant fænomen - superledning af metaller.
Den elektroniske teori om stofstrukturen giver følgende forklaring på stigningen i modstand af metalledere med stigende temperatur.Når den opvarmes, modtager lederen termisk energi, som uundgåeligt overføres til alle atomer af stoffet, som et resultat af, at intensiteten af deres bevægelse øges. Den øgede bevægelse af atomer skaber større modstand mod den rettede bevægelse af frie elektroner, hvorfor lederens modstand øges. Efterhånden som temperaturen falder, skabes der bedre betingelser for retningsbestemt bevægelse af elektroner, og lederens modstand falder. Dette forklarer et interessant fænomen - superledning af metaller.
Superledningsevne Reduktion af modstanden af metaller til nul sker ved en enorm negativ temperatur -273° ° Såkaldt absolut nul. Ved en temperatur på det absolutte nulpunkt ser metalatomer ud til at fryse på plads, fuldstændig uforstyrret af elektronernes bevægelse.
