Hvad er vekselstrøm og hvordan adskiller den sig fra jævnstrøm

Vekselstrøm, I modsætning hertil DC strøm, ændrer sig konstant både i størrelse og retning, og disse ændringer forekommer periodisk, det vil sige, at de gentager sig med nøjagtig lige store intervaller.

For at inducere en sådan strøm i kredsløbet skal du bruge vekselstrømkilder, der skaber en veksel-EMK, der periodisk ændrer sig i størrelse og retning. Sådanne kilder kaldes vekselstrømsgeneratorer.

I fig. 1 viser et apparatdiagram (model) af de simpleste generator. 

En rektangulær ramme lavet af kobbertråd, fastgjort på aksen og roteret i marken ved hjælp af et remtræk magnet… Enderne af rammen er loddet til kobberringe, som roterende med rammen glider på kontaktpladerne (børsterne).

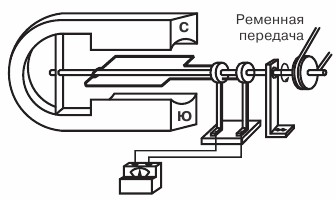
Figur 1. Diagram over den enkleste generator

Lad os sikre os, at en sådan enhed virkelig er en kilde til variabel EMF.

Antag, at en magnet skaber mellem dens poler ensartet magnetfelt, det vil sige en, hvor tætheden af ​​magnetiske feltlinjer i hver del af feltet er den samme.roterende krydser rammen magnetfeltets kraftlinjer i hver af dets sider a og b EMF induceret. 

Rammens sider c og d fungerer ikke, fordi når rammen roterer, krydser de ikke magnetfeltets kraftlinjer og deltager derfor ikke i skabelsen af ​​EMF.

På et hvilket som helst tidspunkt er den EMF, der forekommer på side a, modsat i retning af den EMF, der forekommer på side b, men i rammen virker begge EMF'er i overensstemmelse med og adderer til den totale EMF, det vil sige induceret af hele rammen.

Dette er nemt at kontrollere, hvis vi bruger den højrehåndsregel, vi kender, til at bestemme retningen af ​​EMF.

For at gøre dette skal du placere håndfladen på højre hånd, så den vender mod nordpolen af ​​magneten, og den bøjede tommelfinger falder sammen med bevægelsesretningen på den side af rammen, hvor vi vil bestemme retningen af ​​EMF. Så vil retningen af ​​EMF i den blive angivet af håndens udstrakte fingre.

Uanset hvilken position af rammen, vi bestemmer retningen af ​​EMF i siderne a og b, lægges de altid sammen og danner en samlet EMF i rammen. Samtidig med hver rotation af rammen ændres retningen af ​​den samlede EMF i den til det modsatte, da hver af rammens arbejdssider i en omdrejning passerer under forskellige poler af magneten.

Størrelsen af ​​EMF induceret i rammen ændres også, efterhånden som den hastighed, hvormed siderne af rammen krydser de magnetiske feltlinjer, ændres. Faktisk, i det øjeblik, hvor rammen nærmer sig sin lodrette position og passerer den, er hastigheden af ​​at krydse kraftlinjerne på siderne af rammen den højeste, og den største emk induceres i rammen.På de tidspunkter, når rammen passerer sin vandrette position, ser dens sider ud til at glide langs de magnetiske feltlinjer uden at krydse dem, og der induceres ingen EMF.

Derfor vil der med ensartet rotation af rammen blive induceret en EMF i den, der periodisk ændrer sig både i størrelse og retning.

Den EMF, der forekommer i rammen, kan måles af en enhed og bruges til at skabe en strøm i det eksterne kredsløb.

Ved brug af fænomenet elektromagnetisk induktion, kan du få veksel-EMK og derfor vekselstrøm.

Vekselstrøm til industrielle formål og til belysning produceret af kraftige generatorer drevet af damp- eller vandturbiner og forbrændingsmotorer.

Grafisk gengivelse af AC- og DC-strømme

Den grafiske metode gør det muligt at visualisere processen med at ændre en bestemt variabel afhængig af tid.

At plotte variabler, der ændrer sig over tid, begynder med at plotte to indbyrdes vinkelrette linjer kaldet grafens akser. Derefter, på den vandrette akse, på en bestemt skala, plottes tidsintervaller, og på den lodrette akse, også på en bestemt skala, værdierne af den mængde, der skal plottes (EMF, spænding eller strøm).

I fig. 2 grafiske jævnstrøm og vekselstrøm ... I dette tilfælde forsinker vi strømværdierne og strømværdierne i én retning, som normalt kaldes positive, forsinkes lodret fra skæringspunktet mellem akserne O , og ned fra dette punkt kaldes den modsatte retning, som normalt er negativ.

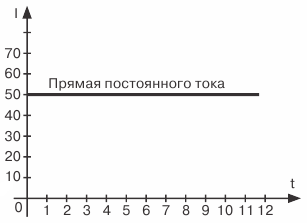
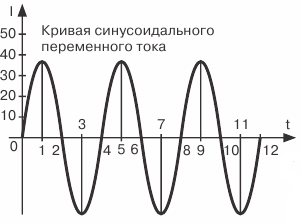Figur 2. Grafisk fremstilling af DC og AC

Punkt O selv tjener både som oprindelsen af ​​aktuelle værdier (lodret ned og op) og tid (vandret til højre).Dette punkt svarer med andre ord til strømmens nulværdi og dette udgangspunkt i tiden, hvorfra vi agter at spore, hvordan strømmen vil ændre sig i fremtiden.

Lad os kontrollere rigtigheden af ​​det, der er plottet i fig. 2 og et 50 mA jævnstrømsplot.

Da denne strøm er konstant, det vil sige, den ikke ændrer sin størrelse og retning over tid, vil de samme strømværdier svare til forskellige tidspunkter, det vil sige 50 mA. Derfor, i det øjeblik, der er lig med nul, det vil sige i det første øjeblik af vores observation af strømmen, vil det være lig med 50 mA. Ved at tegne et segment svarende til den aktuelle værdi på 50 mA på den lodrette akse opad får vi det første punkt på vores graf.

Vi skal gøre det samme i det næste tidspunkt i tiden svarende til punkt 1 på tidsaksen, det vil sige udskyde fra dette punkt lodret opad et segment, der også er lig med 50 mA. Slutningen af ​​segmentet vil definere det andet punkt i grafen for os.

Efter at have lavet en lignende konstruktion for flere efterfølgende tidspunkter opnår vi en række punkter, hvis forbindelse vil give en lige linje, som er en grafisk repræsentation af en konstant strømværdi på 50 mA.

Plotning af en variabel EMF

Lad os gå videre til at studere variabel graf for EMF... I fig. 3 er en ramme, der roterer i et magnetisk felt, vist øverst, og en grafisk repræsentation af den resulterende variable EMF er givet nedenfor.

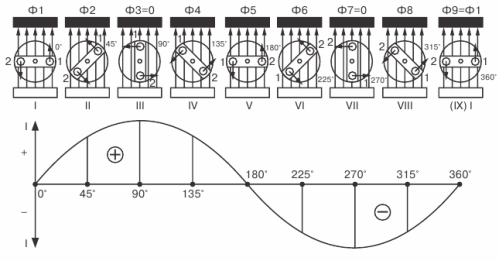Figur 3. Plotning af variablen EMF

Vi begynder at rotere rammen ensartet med uret og følge forløbet af EMF-ændringer i den, idet vi tager rammens vandrette position som det indledende øjeblik.

I dette første øjeblik vil EMF være nul, fordi siderne af rammen ikke krydser de magnetiske feltlinjer.På grafen er denne nulværdi af EMF svarende til tidspunktet t = 0 repræsenteret ved punkt 1.

Med yderligere rotation af rammen vil EMF begynde at dukke op i den og vil stige, indtil rammen når sin lodrette position. På grafen vil denne stigning i EMF være repræsenteret af en jævn stigende kurve, der når sit højdepunkt (punkt 2).

Når rammen nærmer sig den vandrette position, vil EMF i den falde og falde til nul. På grafen vil dette blive afbildet som en faldende glat kurve.

Derfor var EMF i den tid, der svarer til en halv omdrejning af rammen, i stand til at stige fra nul til maksimumværdien og falde til nul igen (punkt 3).

Med yderligere rotation af rammen vil EMF dukke op igen i den og gradvist stige i størrelse, men dens retning vil allerede ændre sig til den modsatte, som det kan ses ved at anvende højrehåndsreglen.

Grafen tager højde for ændringen i retningen af ​​EMF, således at kurven, der repræsenterer EMF, krydser tidsaksen og nu ligger under denne akse. EMF øges igen, indtil rammen indtager en lodret position.

Så vil EMF begynde at falde, og dens værdi vil blive lig med nul, når rammen vender tilbage til sin oprindelige position efter at have gennemført en hel omdrejning. På grafen vil dette komme til udtryk ved, at EMF-kurven når sit højdepunkt i den modsatte retning (punkt 4), så vil møde tidsaksen (punkt 5)

Dette afslutter en cyklus med ændring af EMF, men hvis du fortsætter rotationen af ​​rammen, begynder den anden cyklus straks, nøjagtigt at gentage den første, som igen vil blive efterfulgt af den tredje, derefter den fjerde, og så videre, indtil vi stopper rotationsrammen.

For hver rotation af rammen fuldender EMF'en, der forekommer i den, således en komplet cyklus af dens ændring.

Hvis rammen er lukket til et eksternt kredsløb, vil en vekselstrøm strømme gennem kredsløbet, hvis graf vil se ud som EMF-grafen.

Den resulterende bølgeform kaldes en sinusbølge, og strømmen, EMF eller spændingen, der varierer i henhold til denne lov, kaldes sinusformet.

Selve kurven kaldes en sinusform, fordi den er en grafisk repræsentation af en variabel trigonometrisk størrelse kaldet sinus.

Den sinusformede karakter af strømændringen er den mest almindelige inden for elektroteknik, derfor, når vi taler om vekselstrøm, betyder de i de fleste tilfælde sinusformet strøm.

For at sammenligne forskellige vekselstrømme (EMF'er og spændinger) er der værdier, der karakteriserer en bestemt strøm. Disse kaldes AC-parametre.

Periode, Amplitude og Frekvens — AC-parametre

Vekselstrøm er kendetegnet ved to parametre — månedlig cyklus og amplitude, idet vi ved, at vi kan estimere, hvilken slags vekselstrøm det er, og bygge en graf over strømmen.

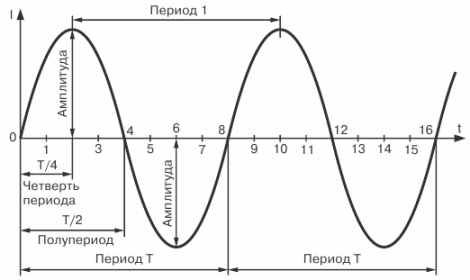
Figur 4. Sinusformet strømkurve

Det tidsrum, i hvilket en komplet cyklus af aktuelle ændringer finder sted, kaldes en periode. Perioden er angivet med bogstavet T og måles i sekunder.

Den periode, hvor halvdelen af ​​en komplet cyklus af strømændringer finder sted, kaldes en halv cyklus. Derfor består perioden med strømændring (EMF eller spænding) af to halve perioder. Det er helt indlysende, at alle perioder af den samme vekselstrøm er ens med hinanden.

Som det kan ses af grafen, når strømmen i løbet af en periode af dens ændring det dobbelte af sin maksimale værdi.

Den maksimale værdi af en vekselstrøm (EMF eller spænding) kaldes dens amplitude eller spidsstrømværdi.

Im, Em og Um er almindelige betegnelser for strøm-, EMF- og spændingsamplituder.

Først og fremmest var vi opmærksomme spidsstrøm, men som det kan ses af grafen, er der utallige mellemværdier, der er mindre end amplituden.

Værdien af ​​vekselstrøm (EMF, spænding) svarende til ethvert valgt tidspunkt kaldes dens øjeblikkelige værdi.

i, e og u er almindeligt accepterede betegnelser for de øjeblikkelige værdier af strøm, emk og spænding.

Den øjeblikkelige værdi af strømmen, såvel som dens spidsværdi, er let at bestemme ved hjælp af grafen. For at gøre dette skal du fra ethvert punkt på den vandrette akse, der svarer til det tidspunkt, vi er interesseret i, tegne en lodret linje til skæringspunktet med den aktuelle kurve; det resulterende segment af den lodrette linje vil bestemme værdien af ​​strømmen på et givet tidspunkt, det vil sige dens øjeblikkelige værdi.

Det er klart, at den øjeblikkelige værdi af strømmen efter tid T / 2 fra grafens startpunkt vil være nul, og efter tid T / 4 dens amplitudeværdi. Strømmen når også sin spidsværdi; men allerede i den modsatte retning, efter en tid svarende til 3/4 T.

Så grafen viser, hvordan strømmen i kredsløbet ændrer sig over tid, og at kun én bestemt værdi af både størrelsen og retningen af ​​strømmen svarer til hvert tidspunkt. I dette tilfælde vil værdien af ​​strømmen på et givet tidspunkt på et punkt i kredsløbet være nøjagtig den samme på ethvert andet punkt i det kredsløb.

Det kaldes antallet af komplette perioder, der opfyldes af strømmen i 1 sekund af AC-frekvensen, og er angivet med det latinske bogstav f.

For at bestemme frekvensen af ​​en vekselstrøm, det vil sige for at finde ud af, hvor mange perioder af dens ændring strømmen foretaget på 1 sekund, er det nødvendigt at dividere 1 sekund med tiden for en periode f = 1 / T. At kende frekvensen af vekselstrømmen, kan du bestemme perioden: T = 1 / f

AC frekvens det måles i en enhed kaldet hertz.

Hvis vi har en vekselstrøm, hvis frekvens er lig med 1 hertz, så vil perioden for en sådan strøm være lig med 1 sekund. Omvendt, hvis ændringsperioden for strømmen er 1 sekund, så er frekvensen af ​​en sådan strøm 1 hertz.

Så vi har defineret AC-parametre – periode, amplitude og frekvens – som giver dig mulighed for at skelne mellem forskellige AC-strømme, EMF'er og spændinger og plotte deres grafer, når det er nødvendigt.

Ved bestemmelse af forskellige kredsløbs modstand mod vekselstrøm anvendes en anden hjælpeværdi, der karakteriserer vekselstrøm, den såkaldte vinkel- eller vinkelfrekvens.

Cirkulær frekvens angivet relateret til frekvens f ved forholdet 2 pif

Lad os forklare denne afhængighed. Da vi plottede den variable EMF-graf, så vi, at en fuldstændig rotation af rammen resulterer i en komplet cyklus af EMF-ændring. Med andre ord, for rammen at lave en omdrejning, det vil sige at rotere 360°, tager det en tid svarende til en periode, det vil sige T sekunder. Så på 1 sekund laver rammen en 360 °/T omdrejning. Derfor er 360 ° / T den vinkel, som rammen roterer igennem på 1 sekund, og udtrykker rammens rotationshastighed, som normalt kaldes vinkel- eller cirkulær hastighed.

Men da perioden T er relateret til frekvensen f med forholdet f = 1 / T, så kan cirkulærhastigheden også udtrykkes som en frekvens og vil være lig med 360 ° f.

Så vi konkluderede, at 360 ° f. For at gøre det nemmere at bruge den cirkulære frekvens til enhver beregning, erstattes vinklen på 360° svarende til en omdrejning af et radialt udtryk svarende til 2pi radianer, hvor pi = 3,14. Så får vi endelig 2pif. Derfor, for at bestemme vinkelfrekvensen af ​​vekselstrøm (EMF eller spænding), skal du gange frekvensen i hertz med et konstant tal 6,28.