Spændingsresonans

Hvis AC-kredsløbet er serieforbundet induktor og kondensator, så påvirker de på hver deres måde generatoren, der fodrer kredsløbet, og faseforbindelserne mellem strøm og spænding.

En induktor introducerer et faseskift, hvor strømmen halter efter spændingen med en fjerdedel af en periode, mens en kondensator tværtimod får spændingen i kredsløbet til at halte strømmen med en fjerdedel af en periode. Effekten af ​​induktiv modstand på faseforskydningen mellem strøm og spænding i et kredsløb er således modsat effekten af ​​kapacitiv modstand.

Dette fører til, at den samlede faseforskydning mellem strøm og spænding i kredsløbet afhænger af forholdet mellem de induktive og kapacitive modstandsværdier.

Hvis værdien af ​​kredsløbets kapacitive modstand er større end den induktive, så er kredsløbet kapacitivt af natur, det vil sige, at spændingen halter efter strømmen i fase. Hvis den induktive modstand i kredsløbet derimod er større end den kapacitive, så leder spændingen strømmen og derfor er kredsløbet induktivt.

Den totale reaktans Xtot for det kredsløb, vi overvejer, bestemmes ved at tilføje den induktive modstand af spolen XL og den kapacitive modstand af kondensatoren XC.

Men da virkningen af ​​disse modstande i kredsløbet er modsat, er en af ​​dem, nemlig Xc, tildelt et minustegn, og den samlede reaktans bestemmes af formlen:

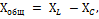
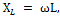
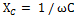
Anvend på dette kredsløb Ohms lov, vi får:

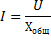
Denne formel kan transformeres som følger:

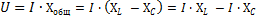
I den resulterende ligning, AzxL - den effektive værdi af komponenten af ​​den samlede spænding af kredsløbet, som vil overvinde den induktive modstand af kredsløbet, og AzNSC - den effektive værdi af komponenten af ​​den samlede spænding af kredsløbet, som vil overvinde den kapacitive modstand.

Således kan den samlede spænding af et kredsløb bestående af en serieforbindelse af en spole og en kondensator betragtes som bestående af to led, hvis værdier afhænger af værdierne af den induktive og kapacitive modstand af kredsløb.

Vi troede, at et sådant kredsløb ikke har nogen aktiv modstand. I tilfælde, hvor kredsløbets aktive modstand ikke længere er så lille, at den er ubetydelig, bestemmes kredsløbets samlede modstand af følgende formel:

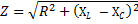
hvor R er den samlede aktive modstand af kredsløbet, XL -NSC - dens samlede reaktans. Går vi til formlen for Ohms lov, har vi ret til at skrive:

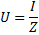
AC spændingsresonans

Induktive og kapacitive modstande forbundet i serie forårsager mindre faseforskydning mellem strøm og spænding i et AC-kredsløb, end hvis de var inkluderet i kredsløbet separat.

Med andre ord, fra den samtidige virkning af disse to reaktioner af forskellig karakter i kredsløbet, sker kompensation (gensidig ødelæggelse) af faseskiftet.

Fuld erstatning, dvs. fuldstændig eliminering af faseforskydningen mellem strøm og spænding i et sådant kredsløb vil ske, når den induktive modstand er lig med kredsløbets kapacitive modstand, dvs. når XL = XC eller, hvilket er det samme, når ωL = 1 / ωC.

I dette tilfælde vil kredsløbet opføre sig som en rent aktiv modstand, det vil sige som om det hverken har en spole eller en kondensator. Værdien af ​​denne modstand bestemmes af summen af ​​de aktive modstande af spolen og forbindelsesledningerne. Ved hvilken effektiv strøm i kredsløbet vil være den største og bestemmes af Ohms lovformel I = U / Rhvor Z nu er erstattet af R.

Samtidig vil spændingerne, der virker på spolen UL = AzxL og på kondensatoren Uc = AzNSCC, være lige store og være så store som muligt. Med lav aktiv modstand i kredsløbet kan disse spændinger mange gange overstige den samlede spænding U af kredsløbsklemmerne. Dette interessante fænomen kaldes spændingsresonans i elektroteknik.

I fig. 1 viser kurverne for spændinger, strømme og effekt ved resonansspændinger i kredsløbet.

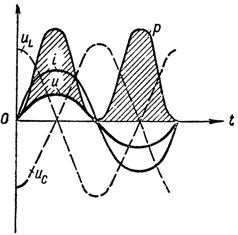
Graf over spændingsstrøm og effekt ved spændingsresonans

Det skal huskes, at modstandene XL og C er variable, der afhænger af strømmens frekvens, og det er værd at ændre dens frekvens en smule, for eksempel at øge den, da XL = ωL vil stige, og XSC = = 1 / ωC vil falde og dermed vil spændingsresonansen i kredsløbet straks blive forstyrret, mens sammen med den aktive modstand vil reaktansen optræde i kredsløbet. Det samme vil ske, hvis du ændrer værdien af ​​kredsløbets induktans eller kapacitans.

Med spændingsresonans vil strømkildens kraft kun blive brugt til at overvinde kredsløbets aktive modstand, det vil sige at opvarme ledningerne.

Faktisk opstår der i et kredsløb med en enkelt induktiv spole energiudsving, dvs. periodisk overførsel af energi fra generatoren til magnetfelt spoler. I et kredsløb med en kondensator sker det samme, men på grund af energien fra kondensatorens elektriske felt. I et kredsløb med en kondensator og en induktor ved spændingsresonans (ХL = XС) passerer energien, når den er lagret af kredsløbet, periodisk fra spolen til kondensatoren og omvendt, og kun det energiforbrug, der er nødvendigt for at overvinde den aktive modstand af kredsløbet falder på andelen af ​​strømkilden. Derfor foregår energiudvekslingen mellem kondensatoren og spolen næsten uden deltagelse af generatoren.

Man skal kun bryde en spændingsresonans efter værdi, hvordan energien i spolens magnetfelt bliver ulig energien fra kondensatorens elektriske felt, og i processen med energiudveksling mellem disse felter vil et overskud af energi vises, som periodisk vil strømme ud fra kilden i kredsløbet, og derefter føre den tilbage til den i kredsløbet.

Dette fænomen minder meget om, hvad der sker i et urværk. Et urs pendul ville være i stand til at svinge uafbrudt uden hjælp fra en fjeder (eller en vægt i en urrullator), hvis det ikke var for friktionskræfterne, der bremser dets bevægelse.

Fjederen, ved at overføre noget af sin energi til pendulet på det rigtige tidspunkt, hjælper den med at overvinde friktionskræfterne og dermed opnå kontinuitet i svingningen.

På samme måde, i et elektrisk kredsløb, når der opstår resonans i det, bruger strømkilden kun sin energi på at overvinde kredsløbets aktive modstand og hjælper dermed den oscillerende proces i det.

Dermed kommer vi til den konklusion, at et vekselstrømskredsløb, bestående af en generator og en serieforbundet induktor og kondensator, under visse betingelser XL = XС bliver til et oscillerende system... Dette kredsløb fik navnet et oscillerende kredsløb.

Fra ligningen XL = XС er det muligt at bestemme værdierne for frekvensen af ​​generatoren, ved hvilken fænomenet spændingsresonans opstår:

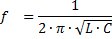
Betyder kapacitans og induktans af kredsløbet, hvor spændingsresonans forekommer:

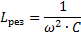
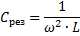
Ved at ændre enhver af disse tre størrelser (eres, L og C) er det således muligt at forårsage spændingsresonans i kredsløbet, det vil sige at omdanne kredsløbet til et oscillerende kredsløb.

Et eksempel på en nyttig anvendelse af spændingsresonans: En modtagers indgangskredsløb justeres af en variabel kondensator (eller variometer) på en sådan måde, at der opstår spændingsresonans i den. Dette opnår en stor stigning i den spolespænding, der kræves til normal modtagerdrift sammenlignet med den kredsløbsspænding, der skabes af antennen.

Sammen med den nyttige brug af fænomenet spændingsresonans i elektroteknik er der ofte tilfælde, hvor spændingsresonans er skadelig En stor stigning i spændingen i individuelle sektioner af kredsløbet (på spolen eller på kondensatoren) sammenlignet med spændingen af generatoren kan føre til beskadigelse af separate dele og måleudstyr.