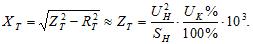Reservekredsløb til transformere ved beregning af elektriske netværk
 Af arten af de opgaver, der skal løses, er beregningerne af elektriske netværk opdelt i to dele:
Af arten af de opgaver, der skal løses, er beregningerne af elektriske netværk opdelt i to dele:
1. Beregninger af netværkstilstande. Det er beregninger af spændinger i knudepunkter, strømme og kræfter i ledninger og transformere med bestemte intervaller.
2. Parametervalgsberegninger. Disse er beregninger af valg af spændinger, parametre for ledninger, transformere, kompensation og andre enheder.
For at foretage ovenstående beregninger skal du først kende de ækvivalente kredsløb, modstand og konduktans af kraftledninger og transformere.
Ved beregninger af elektriske netværk, under hensyntagen til transformere, anvendes i stedet for det T-formede ækvivalente kredsløb, der kendes fra elektroteknik, normalt det enkleste L-formede ækvivalente kredsløb, hvilket i høj grad forenkler beregningerne og ikke forårsager væsentlige fejl . Et sådant ækvivalent kredsløb er vist i fig. 1.
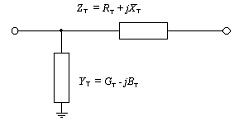
Ris. 1. L-formet transformerækvivalent kredsløb
Hovedparametrene for det ækvivalente kredsløb af en fase af transformeren er den aktive modstand RT, reaktivitet HT, aktiv konduktans GT og reaktiv konduktans BT. Den reaktive konduktans af VT er induktiv af natur. Disse parametre mangler i referencelitteraturen. De bestemmes eksperimentelt i henhold til pasdata: tomgangstab ∆PX, kortslutningstab DRK, kortslutningsspænding UK% og tomgangsstrøm i0%.
For transformere med tre viklinger eller autotransformere er det tilsvarende kredsløb præsenteret i en lidt anderledes form (fig. 2).
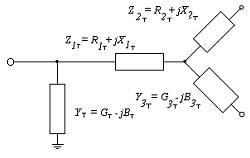
Ris. 2. Tilsvarende kredsløb af en transformer med tre viklinger
I pasdataene for transformere med tre viklinger er kortslutningsspændingen angivet for tre mulige kombinationer: UK1-2%-kortsluttet på mellemspændingsviklingen (MV) og forsyningssiden af højspændingsviklingen (HV). ; UK1-3% — i tilfælde af kortslutning af lavspændingsviklingen (LV) og strømforsyning fra HV-viklingen; UK2-3% — i tilfælde af kortslutning af LV-spolen og forsyningen på HV-siden.
Derudover er versioner af transformeren mulige, når alle tre viklinger er designet til transformerens nominelle effekt, eller når en eller begge sekundære viklinger er designet (med hensyn til opvarmning) til kun 67 % af primærviklingens effekt.
Den aktive og reaktive ledningsevne af det ækvivalente kredsløb bestemmes af formlerne:
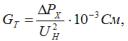
hvor ∆PX — i kW, UN — i kW.
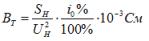
Den samlede aktive modstand af viklingerne RTotot beregnes ved formlen:
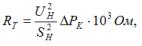
Hvis alle tre viklinger er designet til fuld effekt, tages den aktive modstand af hver af dem ens:
R1T = R2T = R3T = 0,5 RT i alt
Hvis en af de sekundære viklinger er designet til 67% af effekten, tages modstandene af viklingerne, der kan belastes med 100%, lig med 0,5 RTotal. En spole som tillader transmission af 67 % af effekten og hvis tværsnit er 67 % af normalen har en modstand 1,5 gange mere, dvs. 0,75 RTotot.
For at bestemme modstanden af hver af strålerne præsenteres de ækvivalente kredsløb for kortslutningsspændingen som summen af de relative spændingsfald på de enkelte stråler:
UK1-2% = UK1% + UK2%,
UK1-3% = UK1% + UK3%,
UK2-3% = UK2% + UK3%.
Ved at løse dette ligningssystem for UK1% og UK3% får vi:
UK1% = 0,5 (UK1-2% + UK1-3%-UK2-3%),
UK2% = UK1-2% + UK1%,
UK3% = UK1-3% + UK1%.
I praktiske beregninger for en af bjælkerne er spændingsfaldet normalt nul eller en lille negativ værdi. For denne stråle af det ækvivalente kredsløb antages den induktive modstand at være nul, og for de resterende stråler findes de induktive reaktanser afhængigt af de relative spændingsfald med formlen: