Impulsstrøm

I forskellige elektroniske enheder, for eksempel i elektronisk udstyr og halvlederudstyr, det vil sige i forstærkere, ensrettere, radioer, generatorer, fjernsyn, såvel som i kulmikrofoner, telegrafer og mange andre enheder, er de meget udbredte krusningsstrømme og spændinger... for ikke at gentage ræsonnementet to gange, vil vi kun tale om strømme, men alt, der er relateret til strømme, gælder også for spændinger.

Pulserende strømme, der har en konstant retning, men ændrer deres værdi, kan være forskellige. Nogle gange ændres den aktuelle værdi fra den højeste til den laveste værdi, der ikke er nul. I andre tilfælde reduceres strømmen til nul. Hvis jævnstrømskredsløb afbrydes ved en bestemt frekvens, så er der i nogle tidsintervaller ingen strøm i kredsløbet.

I fig. 1 viser grafer for forskellige bølgestrømme. I fig. 1, a, b, sker strømændringen iflg sinusformet kurve, men disse strømme bør ikke betragtes som sinusformede vekselstrømme, da strømmens retning (tegnet) ikke ændres. I fig.1 viser c en strøm bestående af separate impulser, det vil sige kortvarige "chok" af strøm, adskilt fra hinanden ved pauser af større eller mindre varighed, og kaldes ofte pulserende strøm. Forskellige pulserede strømme adskiller sig fra hinanden i formen og varigheden af ​​pulserne, såvel som i gentagelseshastigheden.

Det er praktisk at betragte en pulserende strøm af enhver art som summen af ​​to strømme - jævnstrøm og vekselstrøm, kaldet term- eller komponentstrømme. Enhver pulserende strøm har DC- og AC-komponenter. Det virker mærkeligt for mange. Faktisk er en pulserende strøm en strøm, der hele tiden løber i én retning og ændrer sin værdi.

Hvordan kan du se, at den indeholder vekselstrøm, der ændrer retning? Men hvis to strømme - direkte og vekslende - passerer samtidigt gennem den samme ledning, viser det sig, at der vil løbe en pulserende strøm i den ledning (fig. 2). I dette tilfælde bør amplituden af ​​vekselstrømmen ikke overstige værdien af ​​jævnstrømmen. Jævnstrøm og vekselstrøm kan ikke strømme separat gennem ledningen. De tilføjer til en generel strøm af elektroner, der har alle egenskaberne for en pulserende strøm.

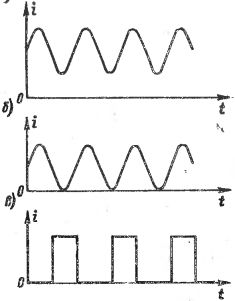
Ris. 1. Grafer over forskellige bølgestrømme

Tilføjelsen af ​​AC- og DC-strømme kan vises grafisk. I fig. 2 viser graferne for en jævnstrøm svarende til 15 mA og en vekselstrøm med en amplitude på 10 mA. Hvis vi summerer værdierne af disse strømme for individuelle tidspunkter under hensyntagen til strømmenes retninger (tegn), får vi bølgestrømgrafen vist i fig. 2 med en fed streg. Denne strøm varierer fra et lavpunkt på 5 mA til et maksimum på 25 mA.

Den overvejede tilføjelse af strømme bekræfter gyldigheden af ​​repræsentationen af ​​den pulserende strøm som summen af ​​jævnstrøm og vekselstrøm. Rigtigheden af ​​denne repræsentation bekræftes også af det faktum, at det ved hjælp af nogle enheder er muligt at adskille komponenterne i denne strøm fra hinanden.

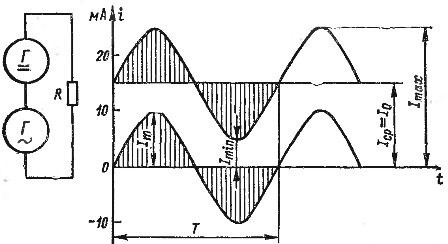
Ris. 2. Opnåelse af en pulserende strøm ved at tilføje jævn- og vekselstrøm.

Det skal understreges, at enhver strøm altid kan repræsenteres som en sum af flere strømme. For eksempel kan en strøm på 5 A betragtes som summen af ​​strømme 2 og 3 A, der flyder i én retning, eller summen af ​​strømme 8 og 3 A, der flyder i forskellige retninger, det vil sige, med andre ord forskellen mellem strømme 8 og 3 A. Det er ikke svært at finde andre kombinationer af to eller flere strømme, der giver i alt 5 A.

Her er der fuldstændig lighed med princippet om addition og nedbrydning af kræfter. Hvis to ligeligt rettede kræfter virker på en genstand, kan de erstattes af en fælles kraft. Kræfter, der virker i modsatte retninger, kan erstattes af en enhedsforskel. Omvendt kan en given kraft altid betragtes som summen af ​​tilsvarende ligeligt rettede kræfter eller forskellen mellem modsat rettede kræfter.

Det er ikke nødvendigt at dekomponere direkte eller sinusformede vekselstrømme til komponentstrømme. Hvis vi erstatter den pulserende strøm med summen af ​​jævn- og vekselstrøm, så ved at anvende de kendte love for jævn- og vekselstrøm på disse komponentstrømme, er det muligt at løse mange problemer og foretage de nødvendige beregninger relateret til pulserende strøm.

Konceptet med pulserende strøm som summen af ​​jævnstrøm og vekselstrøm er konventionelt.Det kan naturligvis ikke antages, at jævn- og vekselstrømmen med bestemte tidsintervaller virkelig løber mod hinanden langs ledningen. Faktisk er der ikke to modsatte strømme af elektroner.

I virkeligheden er en pulserende strøm en enkelt strøm, der ændrer sin værdi over tid. Det er mere korrekt at sige, at den pulserende spænding eller pulserende EMF kan repræsenteres som summen af ​​de konstante og variable komponenter.

For eksempel i fig. 2 viser, hvor algebraisk den konstante emk for en generator adderes til den variable emk af en anden generator. Som et resultat har vi en pulserende EMF, der forårsager den tilsvarende pulserende strøm. Betinget kan det dog overvejes, at en konstant EMF skaber en jævnstrøm i kredsløbet, og en veksel-EMK - en vekselstrøm, som, når den summeres, danner en pulserende strøm.

Hver pulserende strøm kan karakteriseres ved de maksimale og minimale værdier af Itax og Itin, såvel som dens konstante og variable komponenter. Den konstante komponent er angivet med I0. Hvis vekselkomponenten er en sinusformet strøm, så er dens amplitude betegnet med It (alle disse mængder er vist i fig. 2).

Det må ikke forveksles med It og Itax. Den maksimale værdi af den aktuelle bølge Imax bør heller ikke kaldes amplituden. Udtrykket amplitude refererer normalt kun til vekselstrømme. Med hensyn til den pulserende strøm kan vi kun tale om amplituden af ​​dens variable komponent.

Den konstante komponent af den pulserende strøm kan kaldes dens gennemsnitsværdi Iav, det vil sige den aritmetiske gennemsnitsværdi. Faktisk, hvis vi betragter ændringerne i en periode af den pulserende strøm vist i fig.2 ses tydeligt følgende: i den første halvcyklus tilføjes en række værdier til 15 mA-strømmen ved at variere strømkomponenten, varierende fra 0 til 10 mA og tilbage til 0, og i anden halvdel -cyklus trækkes nøjagtig de samme strømværdier fra de nuværende 15 mA.

Derfor er strømmen på 15 mA virkelig gennemsnitsværdien. Da strøm er overførslen af ​​elektriske ladninger gennem ledningens tværsnit, så er Iav værdien af ​​en sådan jævnstrøm, der i en periode (eller i et helt antal perioder) bærer den samme mængde elektricitet som denne pulserende strøm .

For sinusformet vekselstrøm er værdien af ​​Iav pr. periode nul, fordi mængden af ​​elektricitet, der passerer gennem lederens tværsnit i en halvperiode, er lig med mængden af ​​elektricitet, der passerer i den modsatte retning i en anden halvperiode. På graferne for strømme, der viser afhængigheden af ​​strømmen i på tidspunktet t, er mængden af ​​elektricitet, der bæres af strømmen, udtrykt ved arealet af figuren afgrænset af strømkurven, da mængden af ​​elektricitet er bestemt af produkt, at det.

For en sinusformet strøm er arealet af de positive og negative halvbølger ens I den pulserende strøm vist i fig. 2, i løbet af den første halve periode lægges mængden af ​​elektricitet, der bæres af AC-komponenten, til mængden af ​​elektricitet, der bæres af den nuværende Iav (skraveret område i figuren). Og i løbet af den anden halve cyklus trækkes nøjagtig den samme mængde strøm ud. Som et resultat overføres den samme mængde elektricitet gennem hele perioden som med en enkelt jævnstrøm Iav, det vil sige, at arealet af rektanglet Iav T er lig med området afgrænset af bølgestrømkurven.

Således bestemmes den konstante komponent eller den gennemsnitlige værdi af strømmen af ​​overførslen af ​​elektriske ladninger gennem ledningens tværsnit.

Den aktuelle ligning vist i fig. 2 skal naturligvis skrives i følgende form:

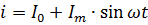
Effekten af ​​den pulserende strøm skal beregnes som summen af ​​effekterne af dens komponentstrømme. For eksempel, hvis strømmen vist i fig. 2, passerer gennem en modstand med modstand R, så er dens effekt

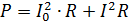
hvor I = 0,7Im er rms værdien af ​​den variable komponent.

Du kan introducere begrebet rms værdien af ​​bølgestrømmen Id. Effekt beregnes på sædvanlig måde:

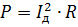
Ved at sidestille dette udtryk med det foregående og reducere det med R, får vi:

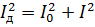
De samme forhold kan opnås for stress.