Uforgrenede og forgrenede lineære elektriske kredsløb med en enkelt forsyning

Hvis et stort antal passive elementer sammen med en kilde til f.eks. etc. c. danner et elektrisk kredsløb, kan deres sammenkobling ske på forskellige måder. Der er følgende typiske skemaer for sådanne forbindelser.

Seriel forbindelse af elementer Dette er den enkleste forbindelse. Med denne forbindelse flyder den samme strøm i alle elementer i kredsløbet. Ifølge dette skema kan enten alle de passive elementer i kredsløbet tilsluttes, og så vil kredsløbet være enkeltkredsløb uforgrenet (fig. 1., a), eller kun en del af elementerne i multikredsløbskredsløbet kan være tilsluttet.

Hvis n elementer er forbundet i serie, hvori den samme strøm I løber, så vil spændingen ved kredsløbets terminaler være lig summen af ​​spændingsfaldene i n elementer forbundet i serie, dvs.

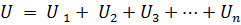
eller:

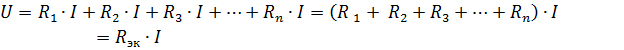
hvor Rek er den ækvivalente kredsløbsmodstand.

Derfor er den ækvivalente modstand af passive elementer forbundet i serie lig med summen af ​​modstandene af disse elementer... Det elektriske skema (fig.1, a) kan der præsenteres et ækvivalent kredsløb (fig. 1, b), bestående af et element med en ækvivalent modstand Rek

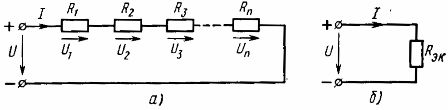
Ris. 1. Skema for seriel forbindelse af lineære elementer (a) og dets tilsvarende skema (b)

Ved beregning af et kredsløb med elementer forbundet i serie ved en given spænding af strømkilden og elementernes modstande, beregnes strømmen i kredsløbet efter Ohms lov:

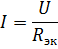
Spændingsfald over det k'te element

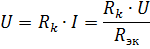
afhænger ikke kun af modstanden af ​​dette element, men også af den ækvivalente modstand Rek, det vil sige modstanden af ​​andre elementer i kredsløbet. Dette er en væsentlig ulempe ved seriel forbindelse af elementer. I det begrænsende tilfælde, når modstanden af ​​ethvert element i kredsløbet bliver lig med uendeligt (åbent kredsløb), bliver strømmen i alle elementer i kredsløbet nul.

Da, når den er forbundet i serie, er strømmen i alle elementer i kredsløbet den samme, er forholdet mellem spændingsfaldet i elementerne lig med forholdet mellem disse elementers modstande:

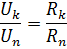
Parallelforbindelse af elementer - dette er en forbindelse, hvor den samme spænding påføres alle elementer i kredsløbet. Ifølge parallelforbindelsesskemaet kan enten alle passive elementer i kredsløbet (fig. 2, a) eller kun en del af dem tilsluttes. Hvert parallelt forbundet element danner en separat gren. Derfor er kredsløbet med parallelforbindelse af elementer vist i fig. 2, a, selvom det er et simpelt kredsløb (da det kun indeholder to knudepunkter), er det samtidig forgrenet.

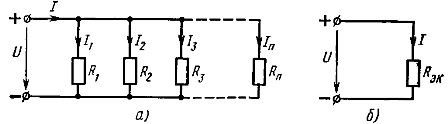
Ris. 2. Skema for parallelforbindelse af lineære elementer (a) og dets tilsvarende skema (b)

I hver parallel gren er strømmen

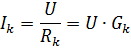
hvor Gk er ledningsevnen af ​​den k'te gren.

Fra Kirchhoffs første lov

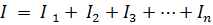
eller

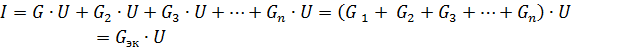
hvor Gec er den ækvivalente kredsløbsledningsevne.

Derfor, når passive elementer er forbundet parallelt, er deres ækvivalente konduktans lig med summen af ​​disse elementers konduktanser... Den ækvivalente konduktans er altid større end konduktansen af ​​nogen del af de parallelle forgreninger. Ækvivalent ledningsevne GEK svarer til ækvivalent modstand Rek = 1 / Gek.

Derefter det tilsvarende kredsløb vist i fig. 2, a, vil have den i fig. 2, b. Strømmen i den uforgrenede del af kredsløbet med parallelforbindelse af elementer kan bestemmes ud fra dette kredsløb i henhold til Ohms lov:

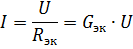
Derfor, hvis forsyningsspændingen er konstant, så med en stigning i antallet af elementer forbundet parallelt (hvilket fører til en stigning i den ækvivalente ledningsevne), stiger strømmen i den uforgrenede del af kredsløbet (strømforsyningsstrømmen).

Fra formlen

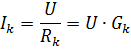
det kan ses, at strømmen i hver gren kun afhænger af konduktansen af ​​den gren og ikke afhænger af konduktansen af ​​andre grene. Uafhængigheden af ​​parallelle forgreningstilstande fra hinanden er en vigtig fordel ved parallelforbindelse af passive elementer. I industrielle installationer anvendes parallelforbindelse af elektriske modtagere i de fleste tilfælde. Det mest oplagte eksempel er inddragelsen af ​​elektriske lamper til belysning.

Da der i en parallelforbindelse påføres den samme spænding til alle elementer, og strømmen i hver gren er proportional med konduktansen af ​​den gren, er forholdet mellem strømme i parallelle grene lig med forholdet mellem konduktanserne af disse grene, eller omvendt proportional til forholdet mellem deres modstande:

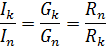
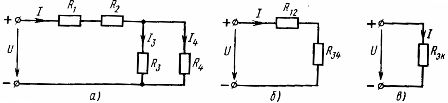
En blandet forbindelse af elementer er en kombination af serie- og parallelforbindelser. En sådan kæde kan have et andet antal knudepunkter og grene. Et eksempel på en blandet forbindelse er vist i diagrammet (fig. 3, a)

Ris. 3. Skema for blandet forbindelse af lineære elementer (a) og dets ækvivalente skemaer (b, c).

For at beregne et sådant kredsløb er det nødvendigt successivt at bestemme de ækvivalente modstande for de dele af kredsløbet, der kun er serie- eller kun parallelforbindelse. I det betragtede kredsløb er der en serieforbindelse af elementer med modstand R1 og R2 og en parallelforbindelse af elementer med modstand R3 og R4. Ved at bruge de tidligere opnåede forhold mellem kredsløbselementernes parametre med deres serie- og parallelforbindelse kan det reelle elektriske kredsløb successivt erstattes af ækvivalente kredsløb.

Ækvivalent modstand af elementer forbundet i serie

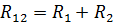
Ækvivalent modstand af parallelforbundne elementer R3 og R4

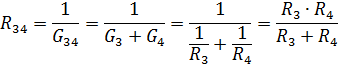
Et ækvivalent kredsløb med modstandene af elementerne R12 og R34 er vist i fig. 3, b. For denne serieforbindelse af R12 og R34 er den tilsvarende modstand

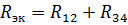
og det tilsvarende ækvivalente kredsløb er vist i fig. 2, b. Lad os finde strømmen i dette kredsløb:

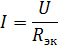
Disse er forsyningsstrømmen og strømmen i elementerne R1 og R2 i det reelle kredsløb.For at beregne strømmene I3 og I4 skal du bestemme spændingen i sektionen af ​​kredsløbet med modstand R34 (fig. 3, b):

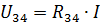
Så kan strømmene I3 og I4 findes ifølge Ohms lov:

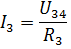
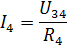
På lignende måde kan man beregne en række andre elektriske kredsløb med blandet tilslutning af passive elementer.

For komplekse kredsløb med et stort antal kredsløb og kilder til f.eks. etc. c. En sådan tilsvarende ombygning kan ikke altid gennemføres. De beregnes efter andre metoder.