Trefaset netforsyning: aktiv, reaktiv, fuld

Værdierne af den samlede aktive og samlede reaktive effekt af det trefasede kredsløb er lig med summen af ​​den aktive og reaktive effekt for hver af henholdsvis de tre faser A, B og C. Denne erklæring er illustreret ved følgende formler:

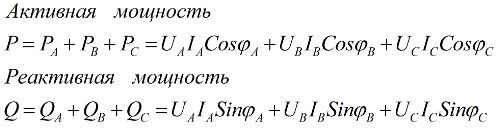
her er Ua, Ub, Uc, Ia, Ib, Ic værdierne for fasespændinger og strømme og φ er faseforskydningen.

Når belastningen er symmetrisk, det vil sige under forhold, hvor den aktive og reaktive effekt af hver af faserne er lig med hinanden, for at finde den samlede effekt af flerfasekredsløbet, er det nok at gange værdien af ​​faseeffekten med antallet af involverede faser. Den samlede effekt bestemmes baseret på de opnåede værdier af dets aktive og reaktive komponenter:

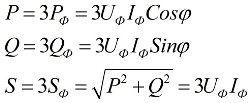
I ovenstående formler kan mængdernes faseværdier udtrykkes i form af deres lineære værdier, som vil være forskellige for stjerne- eller deltaforbindelsesskemaer for brugere, men effektformlerne vil i sidste ende være de samme:

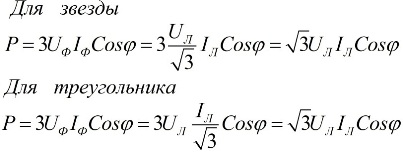
Det følger af ovenstående udtryk, at uanset tilslutningsskemaet for modtagerne af elektrisk energi, uanset om det er en trekant eller en stjerne, hvis belastningen er symmetrisk, vil formlerne til at finde effekten have samme form, både for en trekant og for en stjerne:

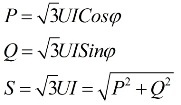
Disse formler viser lineære værdier af spænding og strøm og er skrevet uden abonnenter. Normalt findes en sådan notation, uden subscripts, det vil sige, hvis der ikke er subscripts, så mener vi lineære værdier.

Et særligt måleapparat, kaldet wattmåler… Dens aflæsninger bestemmes af formlen:

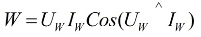
i ovenstående formel er Uw og Iw vektorerne for den spænding, der påføres belastningen og strømmen, der løber gennem den.

Karakteren af ​​den aktive belastning og fasetilslutningsdiagrammet kan være anderledes, derfor vil afhængigt af de specifikke omstændigheder, tilslutningsdiagrammerne for wattmåleren være forskellige.

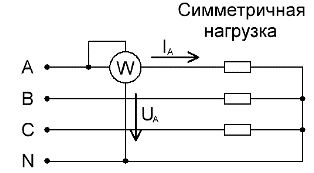
For symmetrisk belastede trefasede kredsløb, for en grov måling af den samlede aktive effekt, hvis høj nøjagtighed ikke er påkrævet, er et wattmeter forbundet til kun en af ​​faserne tilstrækkeligt. Derefter, for at få værdien af ​​den aktive effekt af hele kredsløbet, er det fortsat at multiplicere aflæsningerne af wattmåleren med antallet af faser:

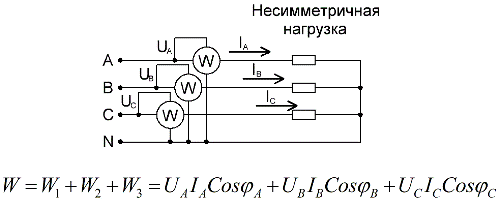
For et fire-leder kredsløb med en neutral ledning, for nøjagtigt at måle aktiv effekt, kræves tre wattmeter, som hver aflæses og derefter summeres for at opnå en værdi for den samlede effekt af kredsløbet:

Hvis der ikke er en neutral ledning i et trefaset kredsløb, er to wattmeter tilstrækkeligt til at måle den samlede effekt, selvom belastningen er ubalanceret.

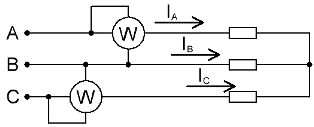
I mangel af en nulleder er fasestrømmene forbundet i henhold til Kirchhoffs første lov:

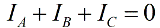
Så vil summen af ​​aflæsningerne af et par wattmeter være lig med:

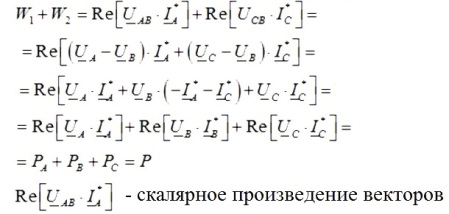
Så hvis du tilføjer aflæsningerne af et par wattmålere, får du den samlede aktive effekt i det trefasede kredsløb, der undersøges, og aflæsningerne af wattmålerne vil afhænge af både størrelsen af ​​belastningen og dens natur.

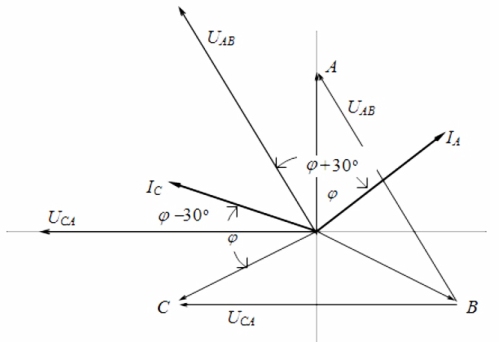
Ser man på vektordiagrammet over strømme og spændinger i forbindelse med en symmetrisk belastning, kan det konkluderes, at aflæsningerne af wattmetre bestemmes af følgende formler:

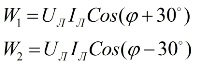
Efter at have analyseret disse udtryk kan det forstås, at med en rent aktiv belastning, når φ = 0, vil aflæsningerne af de to wattmetre være lig med hinanden, det vil sige W1 = W2.

Med aktiv belastningsinduktans, når 0 ≤ φ ≤ 90 °, vil aflæsningerne af wattmeter 1 være mindre end dem for wattmeter 2, det vil sige W1 60 °, vil aflæsningerne af wattmeter 1 være negative, det vil sige W1 <0.

Med en aktiv-kapacitiv karakter af belastningen, når 0 ≥ φ≥ -90 °, vil aflæsningerne af wattmåleren 2 være mindre end wattmåleren 1, det vil sige W1> W2. Ved φ <-60 ° vil aflæsningerne af wattmåleren 2 blive negative.