Hvad er indre modstand

Antag, at der er et simpelt elektrisk lukket kredsløb, der inkluderer en strømkilde, for eksempel en generator, galvanisk celle eller batteri, og en modstand med modstand R. Da strømmen i kredsløbet ikke afbrydes nogen steder, løber den også inde i kilden.

I en sådan situation kan vi sige, at hver kilde har en vis indre modstand, der forhindrer strømmen i at flyde. Denne interne modstand karakteriserer strømkilden og er betegnet med bogstavet r. Til galvanisk celle eller batteri, den interne modstand er modstanden af ​​elektrolytopløsningen og elektroderne, for en generator - modstanden af ​​statorviklingerne osv.

Således er en strømkilde kendetegnet ved både størrelsen af ​​EMF og værdien af ​​dens egen interne modstand r — begge egenskaber indikerer kvaliteten af ​​kilden.

Højspændingselektrostatiske generatorer (såsom Van de Graaf-generatoren eller Wimshurst-generatoren) for eksempel har en enorm EMF målt i millioner af volt, mens deres indre modstand måles i hundredvis af megohm, så de er ikke egnede til at opnå høje strømme.

Tværtimod har galvaniske celler (såsom et batteri) en EMF af størrelsesordenen 1 volt, selvom deres indre modstand er af størrelsesordenen brøker eller højst ti ohm, og derfor kan strømme af enheder og titusvis af ampere opnås fra galvaniske celler.

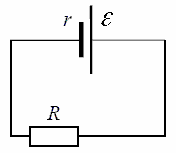
Dette diagram viser en rigtig kilde med en tilsluttet belastning. De er defineret her EMF kilde, dens indre modstand såvel som belastningsmodstand. Ifølge Ohms lov for et lukket kredsløb, vil strømmen i dette kredsløb være lig med:

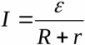
Da den eksterne kredsløbssektion er homogen, kan spændingen over belastningen findes ud fra Ohms lov:

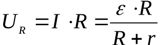
Ved at udtrykke belastningens modstand fra den første ligning og erstatte dens værdi i den anden ligning, opnår vi afhængigheden af ​​spændingen i belastningen af ​​strømmen i et lukket kredsløb:

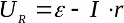
I en lukket sløjfe er EMF lig med summen af ​​spændingsfaldet på de eksterne kredsløbselementer og på selve kildens indre modstand. Belastningsspændingens afhængighed af belastningsstrømmen er ideelt set lineær.

Grafen viser dette, men de eksperimentelle data for en rigtig modstand (kryds i nærheden af ​​grafen) adskiller sig altid fra idealet:

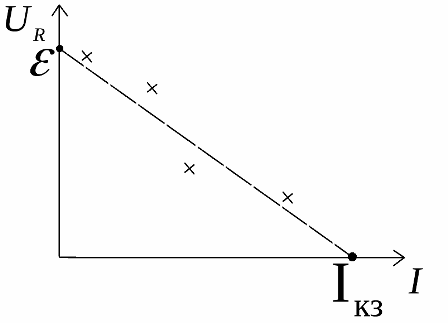
Eksperimenter og logik viser, at ved nul belastningsstrøm er den eksterne kredsløbsspænding lig med kildens emk og ved nul belastningsspænding er kredsløbsstrømmen kortslutningsstrøm… Denne egenskab ved rigtige kredsløb hjælper med eksperimentelt at finde EMF og indre modstand af rigtige kilder.

Eksperimentel påvisning af intern modstand

For eksperimentelt at bestemme disse karakteristika bygges en graf over spændingens afhængighed i belastningen af ​​strømmens størrelse, hvorefter den ekstrapoleres til skæringspunktet med akserne.

I skæringspunktet for grafen med spændingsryggraden er værdien af ​​kildens emf, og i skæringspunktet med strømaksen er værdien af ​​kortslutningsstrømmen. Som et resultat findes den indre modstand ved formlen:

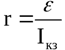
Den nyttige effekt udviklet af kilden fordeles over belastningen. Grafen over denne effekts afhængighed af belastningsmodstanden er vist på figuren. Denne kurve starter fra skæringspunktet mellem koordinatakserne ved nulpunktet, stiger derefter til den maksimale effektværdi og falder derefter til nul med en belastningsmodstand lig med uendelig.

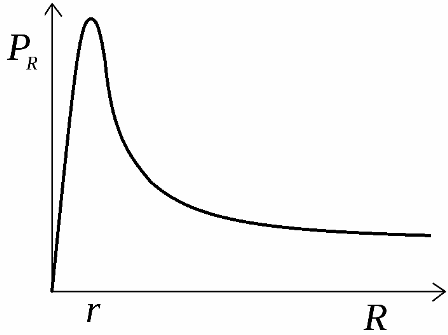
For at finde den maksimale belastningsmodstand, ved hvilken teoretisk maksimal effekt vil blive udviklet med en given kilde, tages den afledede af effektformlen med hensyn til R og indstilles til nul. Maksimal effekt vil blive udviklet, når den eksterne kredsløbsmodstand er lig med den interne kildemodstand:

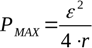
Denne bestemmelse for den maksimale effekt ved R = r giver dig mulighed for eksperimentelt at finde kildens indre modstand ved at plotte den frigivne effekt ved belastningen kontra værdien af ​​belastningsmodstanden.At finde en faktisk snarere end teoretisk belastningsmodstand, der giver maksimal effekt, bestemmer den faktiske interne modstand i strømforsyningen.

Effektiviteten af ​​strømkilden angiver forholdet mellem den maksimale effekt fordelt på belastningen og den samlede effekt, der aktuelt udvikles

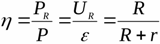
Det er klart, at hvis kilden udvikler en sådan effekt, at den maksimalt mulige effekt for en given kilde opnås ved belastningen, så vil kildens virkningsgrad være lig med 50%.