Ohms lov for et magnetisk kredsløb

Hvis der ikke var nogen magnetiske fluxer, er det usandsynligt, at moderne elektroteknik ville eksistere. Driften af ​​generatorer og elektriske motorer, elektromagneter og transformere, måleinstrumenter og Hall-sensorer er baseret på brugen af ​​magnetfeltet og egenskaberne af den magnetiske flux.

For at koncentrere og styrke den magnetiske flux tyer de til brugen af ​​ferromagnetiske materialer. Ferromagnetiske materialer fremstilles magnetiske kerner — legemer af de krævede former og størrelser, kerner til at lede magnetiske flux af en eller anden størrelse i den krævede retning. Sådanne legemer, inden for hvilke lukkede linjer af magnetisk induktion passerer, kaldes magnetiske kredsløb.

Magnetfeltets kendte egenskaber gør det muligt at beregne de magnetiske fluxer i forskellige magnetiske kredsløb. Men for praktisk arbejde er det meget mere bekvemt at ty til generelle konsekvenser og love for magnetiske kredsløb, der er afledt af magnetfeltets love, i stedet for at bruge disse love direkte hver gang. Anvendelse af visse regler på magnetiske kredsløb er mere praktisk til at løse typiske praktiske problemer.

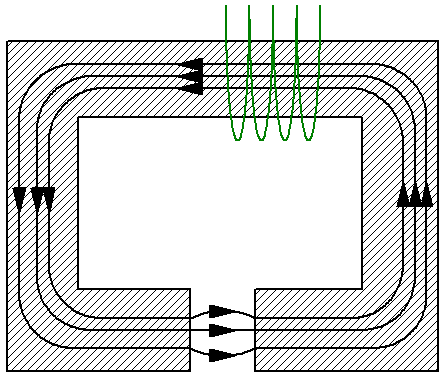
Overvej for eksempel et simpelt magnetisk kredsløb, der består af et uforgrenet åg med tværsnit S, som igen er lavet af et materiale med permeabilitet mu… Åget har et ikke-magnetisk mellemrum med samme areal S, for eksempel luft, og den magnetiske permeabilitet i mellemrummet — mu1 — er forskellig fra ågets magnetiske permeabilitet. Her kan du se på middelinduktionslinjen og anvende den magnetiske spændingssætning på den:

Da linjerne med magnetisk induktion er kontinuerlige gennem hele kredsløbet, er størrelsen af ​​den magnetiske flux i både åget og mellemrummet den samme. Nu bruger vi formlerne til magnetisk induktion B og for den magnetiske flux F til at udtrykke styrken H af det magnetiske felt i form af den magnetiske flux F.

Det næste trin er at erstatte de resulterende udtryk i ovenstående formel for magnetisk fluxsætning:

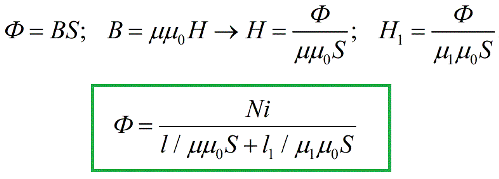
Vi fik en formel, der ligner meget den, der kendes inden for elektroteknik Ohms lov for en del af et lukket kredsløb, og EMF'ens rolle her spilles af størrelsen iN, kaldet den magnetomotoriske kraft (eller MDF) i analogi med den elektromotoriske kraft. I SI-systemet måles magnetomotorisk kraft i ampere.

Summen i nævneren er ikke andet end en analogi af den samlede elektriske modstand for et elektrisk kredsløb, og for et magnetisk kredsløb kaldes det tilsvarende den samlede magnetiske modstand. Udtrykkene i nævneren er de magnetiske modstande af individuelle sektioner af det magnetiske kredsløb.

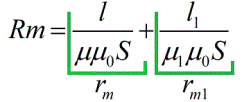
Magnetiske modstande afhænger af længden af ​​det magnetiske kredsløb, dets tværsnitsareal og den magnetiske permeabilitet (svarende til elektrisk ledningsevne for den sædvanlige Ohms lov).Som et resultat kan du skrive formlen for Ohms lov, kun for et magnetisk kredsløb:

Det vil sige, at formuleringen af ​​Ohms lov i forhold til et magnetisk kredsløb lyder sådan her: «i et magnetisk kredsløb uden forgrening er den magnetiske flux lig med kvotienten af ​​divideringen af ​​MDS med kredsløbets totale magnetiske modstand.»

Det fremgår af formlerne, at den magnetiske modstand i NE måles i weber ampere, og den samlede magnetiske modstand af et magnetisk kredsløb er numerisk lig med summen af ​​de magnetiske modstande af delene af det magnetiske kredsløb.

Den beskrevne situation gælder for et uforgrenet magnetisk kredsløb, der omfatter et vilkårligt antal dele, forudsat at den magnetiske flux successivt trænger ind i alle disse dele. Hvis de magnetiske kerner er forbundet i serie, så findes den samlede magnetiske modstand ved at addere delenes magnetiske modstande.

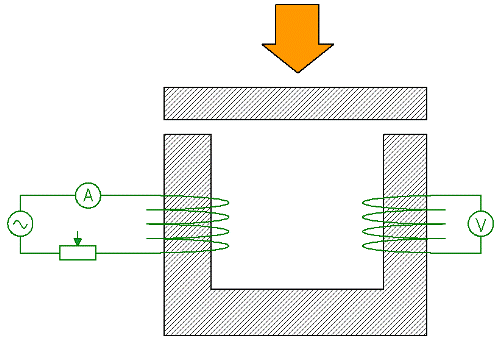
Betragt nu et eksperiment, der demonstrerer effekten af ​​reluktansen af ​​dele af et kredsløb på den totale reluktans af et kredsløb Et U-formet magnetisk kredsløb magnetiseres af spole 1, som tilføres (vekselstrøm) gennem et amperemeter og en rheostat. En EMF induceres i sekundærviklingen 2, og aflæsningerne af voltmeteret forbundet med viklingen er som bekendt proportionale med den magnetiske flux i det magnetiske kredsløb.

Hvis man nu holder strømmen i primærviklingen uændret ved at regulere den med en reostat, og samtidig presser jernpladen mod magnetkredsløbet ovenover, efter at kredsløbets samlede magnetiske modstand vil være stærkt reduceret, vil aflæsningen af voltmeter vil stige tilsvarende.

Selvfølgelig er ovenstående udtryk, såsom "magnetoresistens" og "magnetomotorisk kraft", formelle begreber, da intet i den magnetiske flux bevæger sig, der er ingen bevægelige partikler, det er kun en visuel repræsentation (som en væskestrømsmodel) af en klarere forståelse af lovene...

Den fysiske betydning af ovenstående eksperiment og andre lignende eksperimenter er at forstå, hvordan indførelsen af ​​ikke-magnetiske huller og magnetiske materialer i det magnetiske kredsløb påvirker den magnetiske flux i det magnetiske kredsløb.

Ved at indføre for eksempel en magnet i et magnetisk kredsløb, tilføjer vi yderligere molekylære strømme til de kroppe, der allerede er indeholdt i kredsløbet, som introducerer yderligere magnetiske fluxer. Formelle begreber som "magnetisk modstand" og "magnetomotorisk kraft" viser sig at være meget praktiske, når man løser et praktisk problem, hvorfor de med succes anvendes i elektroteknik.