Tilslutningsdiagrammer over trefasede kredsløb i elektriske netværk

Fordelene ved trefasede netværk, der sikrer deres brede distribution, er indlysende:

• energi overføres over tre ledninger over lange afstande mere økonomisk, end hvis der var færre faser;

• synkrone generatorer, asynkrone motorer, trefasede transformere - lette at fremstille, økonomisk og pålidelige i drift;

• Endelig har et trefaset AC-system evnen til at levere (og tage) konstant øjeblikkelig strøm i en periode med sinusformet strøm, hvis den trefasede generatorbelastning er den samme i alle faser.

Lad os se på, hvilke grundlæggende trefasede kredsløb der findes i elektriske netværk.

Vindingerne på en trefaset generator kan generelt forbindes med belastninger på forskellige måder. Så den mest økonomiske måde ville være at forbinde en separat belastning direkte til hver fase af generatoren ved at forlænge to ledninger for hver belastning. Men med denne tilgang vil der være brug for seks ledninger for at forbinde.

Dette er meget spild med hensyn til materialeforbrug og ubelejligt.For at opnå materialebesparelser kombineres viklingerne af en trefaset generator simpelthen i et «stjerne» eller «delta» kredsløb. Med denne ledningsløsning opnås maksimalt 4 ("stjerne med nulpunkt" eller "delta") eller minimum 3.

En trefaset generator er afbildet på diagrammer i form af tre viklinger placeret i vinkler på 120 ° til hinanden. Hvis forbindelsen af ​​generatorens viklinger udføres i henhold til "stjerne" -skemaet, er terminalerne med samme navn på viklingerne forbundet med hinanden på et punkt (det såkaldte "nulpunkt" af generatoren ). Nulpunktet er markeret med bogstavet «O», og viklingernes frie klemmer (faseklemmer) er markeret med bogstaverne «A», «B» og «C».

Hvis generatorens viklinger er forbundet med hinanden i et "trekant" -skema, er slutningen af ​​den første vikling forbundet med begyndelsen af ​​den anden vikling, slutningen af ​​den anden vikling - til begyndelsen af ​​den tredje, slutningen af ​​den tredje - til begyndelsen af ​​den første - trekanten er lukket. Geometrisk vil summen af ​​EMF i en sådan trekant være nul. Og hvis belastningen slet ikke er forbundet til terminalerne «A», «B» og «C», vil strømmen ikke flyde gennem generatorens viklinger.

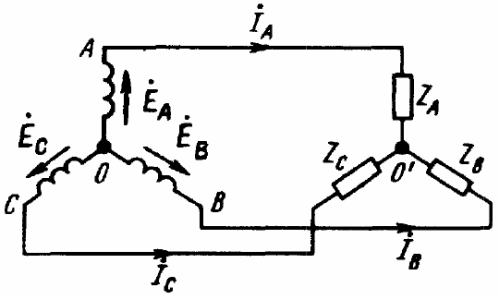
Som et resultat får vi fem grundlæggende skemaer til tilslutning af en trefaset generator med en trefaset belastning (se figurerne). I kun tre af disse figurer kan man se en stjerneforbundet trefaset belastning, hvor de tre ender af belastningen er kombineret i et enkelt punkt. Dette punkt i centrum af belastningsstjernen kaldes «belastningsnulpunkt» og er markeret med «O'».

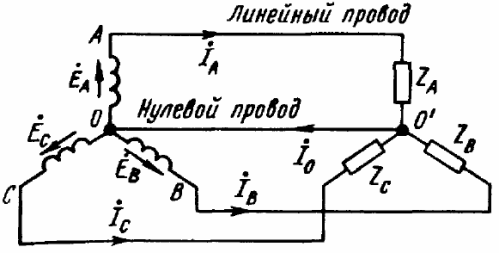
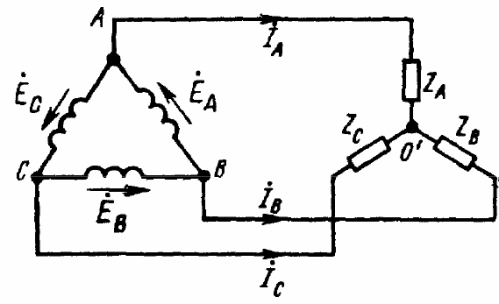
Lederen, der forbinder belastningens nulpunkter og generatoren, kaldes nullederen i sådanne kredsløb. Strømmen af ​​den neutrale ledning er betegnet som «Io».For den positive retning af strømmen tages retningen fra belastningen til generatoren normalt, det vil sige fra punktet «O'» til punktet «O».

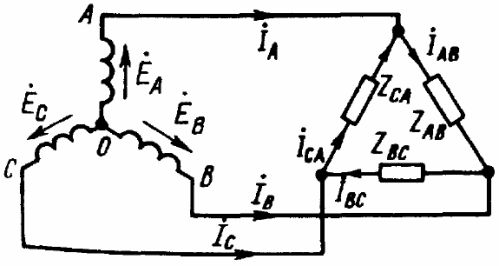
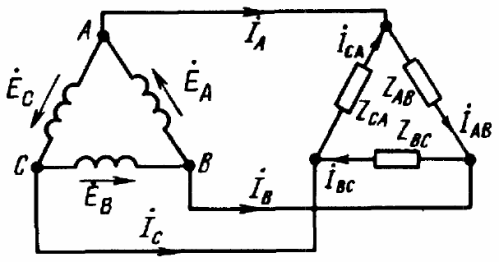
Ledningerne, der forbinder punkterne "A", "B" og "C" på generatorterminalerne med belastningen kaldes linjeledninger, og kredsløbene henholdsvis: stjerne-stjerne med neutral ledning, stjerne-stjerne, stjerne-trekant, delta- delta, delta-stjerne - kun fem grundlæggende ordninger til tilslutning af trefasede kredsløb i elektriske netværk.

Strømme, der strømmer gennem lineære ledere, kaldes lineære strømme og betegnes med Ia, Ib, Ic. For den positive retning af linjestrømmen tages normalt retningen fra generatoren til belastningen. Modulværdierne for linjestrømmene betyder Il, som regel uden yderligere indeks, da det ofte sker, at alle linjestrømmene af kredsløbet er lige store. Spændingen mellem to lineære ledere er den lineære spænding, betegnet med Uab, Ubc, Uca eller, hvis vi taler om modul, skriver de blot Ul.

Hver af generatorviklingerne kaldes en generatorfase, og hver af de tre dele af en trefaset belastning kaldes en belastningsfase. Strømmene i generatorens faser og følgelig af belastningerne kaldes fasestrømme, betegnet med If. Generatorfasernes og belastningsfasernes interne spændinger kaldes fasespændinger, de betegnes Uf.

Hvis generatorens viklinger er forbundet i en «stjerne», så er linjespændingerne 3 gange roden (1,73 gange) højere i absolut værdi end fasespændingerne. Dette skyldes, at liniespændingerne geometrisk bliver til basis i ligebenede trekanter med spidse vinkler i bunden på 30°, hvor benene er fasespændingerne.Bemærk venligst, at en række lave trefasede spændinger: 127, 220, 380, 660 — simpelthen dannes ved at gange den foregående værdi med 1,73.

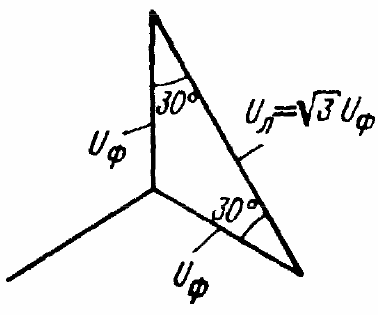
Når generatorens viklinger er forbundet i "stjerne", er linjestrømmen åbenbart lig med fasestrømmen. Men hvad sker der med spændingerne, når generatorviklingerne er tredelt? I dette tilfælde vil netværksspændingen være lig med fasespændingen for hver fase og for hver del af belastningen: Ul = Uf. Når belastningen er stjernekoblet, vil linjestrømmen være lig med fasestrømmen: Il = If.

Når belastningen er forbundet i henhold til "delta"-skemaet, for den positive retning af strømmene, skal du vælge retningen med uret af delta-bypasset. Bestemmelsen foretages af de relevante indekser: fra hvilket punkt strømmen løber, og til hvilket punkt den løber, for eksempel er Iab betegnelsen for strømmen fra punkt "A" til punkt "B".

Hvis en trefaset belastning er delta-forbundet, vil linjestrømmene og fasestrømmene ikke være ens med hinanden. Linjestrømme detekteres derefter af fasestrømme efter Kirchhoffs første lov: Ia = Iab-Ica, Ib = Ibc-Iab, Ic = Ica-Ibc.