Kredsløbstopologier—Grundlæggende begreber

Et elektrisk kredsløb er et sæt af enheder (elementer) og deres forbindelsesledninger, gennem hvilke en elektrisk strøm kan strømme. Alle elementer i elektriske kredsløb deler i passiv og aktiv.

Aktive elementer omdanner forskellige typer energi (mekanisk, kemisk, lys osv.) til elektrisk energi. I passive enheder omdannes elektrisk energi til andre typer energi. Aktive elementer kaldes kilder, passive kaldes forbrugere eller modtagere.

I kredsløbsteori betragtes idealiserede modeller af elektriske elementer. Dette gør beskrivelsen af ​​elementerne så enkel som muligt. Mere komplekse, virkelige elementer er modelleret ud fra et sæt idealiserede elementer.

De vigtigste passive elementer i elektriske kredsløb er modstand (resistivt element), induktor (induktivt element) og kondensator (kapacitivt element). Elementer er installeret i et elektrisk kredsløb for at generere spænding og strøm af en given værdi og form (se - Elektrisk kredsløb og dets elementer).

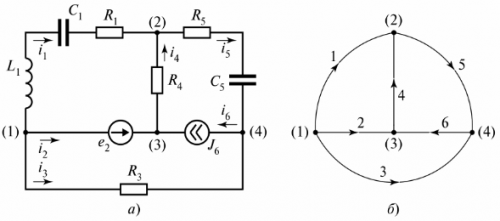
Et elektrisk kredsløb består af grene og knudepunkter. Afdeling — dette er en del af et elektrisk kredsløb (kredsløb), hvorigennem den samme strøm løber. En knude — tilslutning af tre eller flere grene. På det elektriske diagram er knudepunktet angivet med en prik (fig. 1).

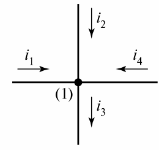
Ris. 1. Definer knudepunktet i diagrammet

Om nødvendigt nummereres diagrammets noder fra venstre mod højre fra top til bund.

I fig. 2 viser den resistiv-kapacitive gren, hvori strømmen iC flyder.

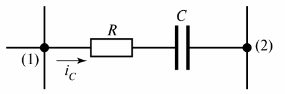
Ris. 2. Resistiv-kapacitiv gren

En anden definition af en gren kan gives - det er en sektion af et kredsløb mellem to tilstødende knudepunkter (knudepunkter (1) og (2) i fig. 2).

Kæde Er der nogen lukket vej i det elektriske kredsløb. Kredsløbet kan lukkes af alle grene, inklusive betingede grene, hvis modstand er lig med uendelig.

I fig. 3 viser et forgrenet elektrisk kredsløb, der består af tre grene.

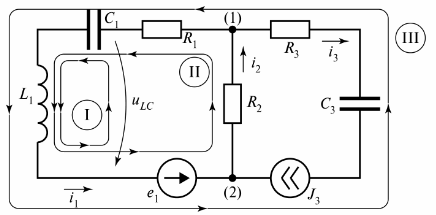
Ris. 3. Elektrisk kredsløb med to kredsløb

Diagrammet viser tre kredsløb, og kredsløb I er lukket af en gren med uendelig modstand. Denne gren er angivet som spænding tiLC.

For kredsløbet i fig. 3 er det muligt at komponere mange sløjfer, der er lukket af reelle eller betingede forgreninger, men til beregning af elektrisk støj bruges begrebet «uafhængig sløjfe». Antallet af uafhængige kredsløbssløjfer er altid indstillet som det minimum, der kræves til beregningen.

Uafhængige kredsløb er altid lukkede, men grene, der har en modstand, der ikke er lig med uendelig, og hvert uafhængigt kredsløb omfatter mindst en gren, der ikke er inkluderet i andre kredsløb. For komplekse elektriske kredsløb kan du bestemme antallet af uafhængige kredsløb ved hjælp af kredsløbsdiagrammet.

På kredsløbsdiagrammet en betinget repræsentation af kredsløbet kaldes, hvor hver gren er erstattet af et linjestykke. Elementer i filialer vises ikke. For eksempel i fig. 4 viser et forgreningskredsløb og dets diagram.

Ris. 4. Forgrenet elektrisk kredsløb: a — kredsløbsdiagram, b — diagram

For at lave et diagram af et diagram, skal du forbinde knudepunkterne med forgreningslinjer uden at angive elementer på dem. Grenene er nummererede, og retningerne af strømmene på dem er angivet med pile. Selve grafen har ingen fysisk betydning, men kan bruges til at bestemme antallet og typen af ​​uafhængige konturer. Til dette formål udarbejdes et "grafisk træ".

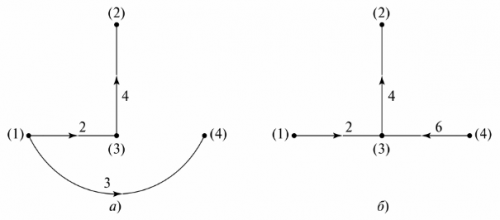
Grafisk træ Det repræsenterer grafen for et kredsløb, hvis knudepunkter er forbundet med forgreninger på en sådan måde, at der ikke er nogen lukket sløjfe. Der kan være flere muligheder for at vise et grafisk træ. I fig. 5 viser to mulige muligheder for kredsløbet i fig. 4.

Ris. 5. Grafisk træ af ordningen

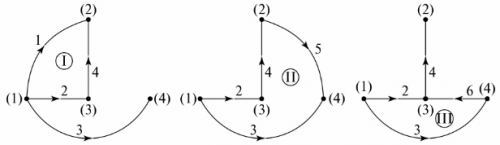
Antallet af manglende grene i graftræet er lig med antallet af uafhængige sløjfer i kredsløbet. I eksemplet er disse tre grene, tre uafhængige sløjfer. Konfigurationen af ​​uafhængige sløjfer kan opnås ved sekventielt at forbinde graftræets noder med grene, der ikke er specificeret på graftræet. For eksempel, for graftræet i fig. 5, og de uafhængige konturer er vist i fig. 6.

Ris. 6. Bestemmelse af uafhængige konturer gennem graftræet

Valget af en mulighed for at konfigurere uafhængige kredsløb til beregning af kredsløbet udføres under kredsløbsanalyse. Du bør vælge sådanne konturer, så beregningen er så enkel som muligt, dvs. antallet af afhængige ligninger i systemet er minimalt.

Topologiske ligninger etablerer en sammenhæng mellem spændinger og strømme i et kredsløb, og antallet og typen af ​​ligninger afhænger ikke af, hvilke elementer der indgår i grenene. Topologiske ligninger omfatter ligninger sammensat af efter Kirchhoffs love.