Effektforhold i det enkleste elektriske kredsløb

I denne artikel vil vi forstå, hvad forholdet mellem kilde- og modtagerparametrene skal være for at opnå den optimale driftsform for det elektriske kredsløb. Effektforhold er også vigtige for lavstrømsteknologier. Disse spørgsmål kan i princippet løses ved hjælp af eksemplet det enkleste elektriske kredsløb.

Kredsløbet består af en jævnstrømskilde med EMF E og intern modstand Rwatt, som genererer elektrisk energi, og en modtagende energimodtager med belastningsmodstand Rn.

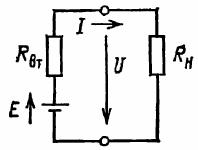
Ris. 1. Skematisk forklaring af effektforholdet i det enkleste kredsløb

Da kilden har indre modstand, bliver noget af den elektriske energi, den udvikler, omdannet til selve varmeenergien.

Strømmen i kredsløbet vist i fig. 1

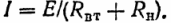
Baseret på denne ligning bestemmer vi modtagerens effekt (kraften til at konvertere elektrisk energi til andre typer):

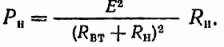
På samme måde er strømtabene i kilden:

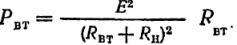
Kildens elektriske effekt skal være lig med summen af ​​effekterne omregnet til andre typer i kilden og modtageren, dvs. der skal være en strømbalance (som for alle kredsløb):

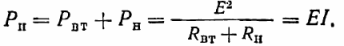
Klemmespændingen U kan også indtastes i udtrykket for effekten Pn.

Modtager strøm:

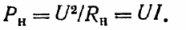
Ydelseskoefficient (COP), defineret som forholdet mellem modtagereffekt (nyttig) og udviklet effekt:

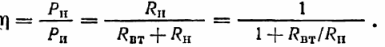
Ligningen viser, at effektivitet afhænger af forholdet mellem belastningsmodstand og indre modstand. Værdierne af disse modstande er den afgørende faktor i fordelingen af ​​kraften udviklet af kilden:

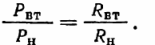
Effekten Pn bør betragtes som nyttig, effekttabene i kilden Pvt bestemmer kun opvarmningen af ​​kilden, og derfor bruges den tilsvarende energi uproduktivt.

Effektiviteten øges med stigende Rn/Rvt-forhold.

For at opnå en stor effektivitetsværdi skal forholdet Pn> Pwt være opfyldt, det vil sige, at kredsløbet skal fungere i en tilstand tæt på til kildens inaktive tilstand.

I praksis kan der stilles to forskellige krav til effektforhold: høj effektivitet og effekttilpasning. Kravet til høj virkningsgrad stilles fx, når det er nødvendigt at overføre en stor mængde energi over ledninger eller at omdanne denne energi til elektriske maskiner. Selv en lille stigning i effektiviteten giver store besparelser i sådanne tilfælde.

Da brugen af ​​høje energier hovedsageligt er karakteristisk for teknikken med høje strømme, er det derfor i dette felt nødvendigt at arbejde i tilstande tæt på tomgangstilstanden.Derudover, når man arbejder i sådanne tilstande, afviger terminalspændingen kun lidt fra kildens emf.

I svagstrømsteknologi (især inden for kommunikationsteknologi og måleteknologi) anvendes meget lave strømkilder, som desuden har store indre modstand… I sådanne tilfælde er effektiviteten, der kendetegner krafttransmissionsprocessen, ofte af underordnet betydning, og kravet om den størst mulige værdi af den effekt, modtageren modtager, understreges.

Mens i højstrømsteknologi ubrugelige eller endda skadelige energiomdannelser - energitab reduceres med stigende effektivitet, øges effektiviteten ved brug af anlæg og enheder i svagstrømsteknologi med den korrekte koordinering af kræfter i elektriske kredsløb.

Betingelsen for at opnå den maksimalt mulige modtagereffekt Pvmax fra en kilde med EMF og interne modstandsdata:

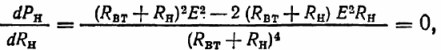
Det følger heraf, at betingelsen for modtagerens maksimale effekt er opfyldt under forudsætning af ligheden Rn = RВt

Når modtagerens modstande og kildens indre modstand er ens, er den effekt modtaget af modtageren således maksimal.

Hvis Rn = Rw, så

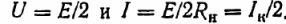
For den effekt modtaget af modtageren har vi:

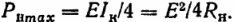
Et eksempel. Med hjælpen termoelektrisk konverter (termoelementer) med en intern modstand Rw = 5 ohm, kan du få en spænding på 0,05 mV / ° C. Den største temperaturforskel er 200 ° C. Hvilke elektriske data skal en indikerende elektrisk enhed have (modstand, effekt, strøm), hvis ønsker at få maksimal effekt fra konverteren.

Giv en løsning på to tilfælde:

a) enheden er forbundet direkte til konverteren;

b) enheden forbindes med to kobbertråde med længde l= 1000 m hver med et tværsnitsareal C = 1 mm2.

Svar. Den maksimale spænding ved terminalerne på den termoelektriske konverter er lig med dens EMF E = 200 * 0,05 = 10 mV.

I dette tilfælde skal indikationen for den enhed, der er tilsluttet kredsløbet, være maksimal (ved den øvre målegrænse).

a) For at enhedens effekt skal være maksimal, er det nødvendigt at matche enhedens og konverterens modstande. Til dette formål vælger vi enhedens modstand svarende til termoelementets modstand, dvs. Rn = Rt = 5 ohm.

Vi finder den maksimale effekt af enheden:

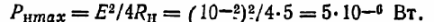
Bestem strømmen:

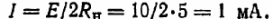
b) Hvis modstanden af ​​ledningerne ikke kan negligeres, skal den tages i betragtning ved bestemmelse af den samlede interne modstand af en aktiv to-terminal enhed bestående af et termoelement og to ledninger, da der ellers er et misforhold mellem modtageren og kilde med hensyn til strøm.

Lad os finde modstanden af ​​ledningerne, givet at den specifikke modstand er 0,0178 μOhm-m:

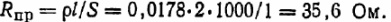
Således er det nødvendige modstandsniveau for enheden:

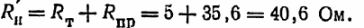
Ved denne værdi af intern modstand vil enhedens effekt være maksimal

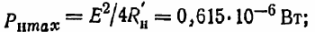
Kredsstrøm:

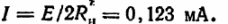
De opnåede resultater viser, at det er tilrådeligt at vælge kilder med en lav værdi af intern modstand, og tværsnitsarealet af forbindelsesledningerne skal være stort nok.

Meget ofte, når der udføres sådanne målinger, kommer beregningen af ​​sammenfaldet af modtageren og kilden ned på, at der fra de tilgængelige instrumenter vælges den, der for en given eller kendt maksimumværdi af den målte værdi opnår den største afbøjning af pilen og giver derfor den største skalaaflæsningsnøjagtighed.