Tidskonstanten for et elektrisk kredsløb - hvad det er, og hvor det bruges

Periodiske processer er iboende i naturen: dag efterfølges af nat, den varme årstid erstattes af kulden osv. Perioden for disse begivenheder er næsten konstant og kan derfor nøje bestemmes. Desuden er vi berettiget til at hævde, at de periodiske naturlige processer, der er nævnt som et eksempel, ikke afskrives, i det mindste med hensyn til en persons levetid.

Men inden for teknologi, inden for elektroteknik og elektronik, især, er ikke alle processer periodiske og kontinuerlige. Normalt stiger nogle elektromagnetiske processer først og falder derefter. Ofte er stof kun begrænset til fasen af ​​begyndelsen af ​​oscillationen, som ikke har tid til rigtig at tage fart.

Ganske ofte kan man inden for elektroteknik finde såkaldte eksponentielle transienter, hvis essens er, at systemet blot stræber efter at nå en eller anden ligevægtstilstand, som til sidst ligner en hviletilstand. En sådan overgang kan enten være stigende eller faldende.

Den ydre kraft bringer først det dynamiske system ud af ligevægt, og forhindrer derefter ikke dette systems naturlige tilbagevenden til dets oprindelige tilstand. Denne sidste fase er den såkaldte overgangsproces, som er karakteriseret ved en vis varighed. Derudover er processen med at ubalancere systemet også en forbigående proces med en karakteristisk varighed.

På den ene eller anden måde, tidskonstanten for den transiente proces, kalder vi dens tidskarakteristik, som bestemmer den tid, efter hvilken en bestemt parameter i denne proces vil ændre tiderne «e», det vil sige, den vil stige eller falde med omkring 2,718 gange sammenlignet med den oprindelige tilstand.

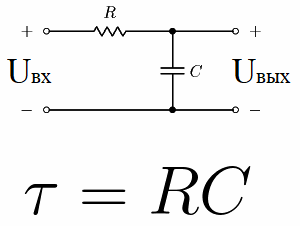
Overvej for eksempel et elektrisk kredsløb bestående af en jævnspændingskilde, en kondensator og en modstand. Denne type kredsløb, hvor en modstand er forbundet i serie med en kondensator, kaldes et RC-integrationskredsløb.

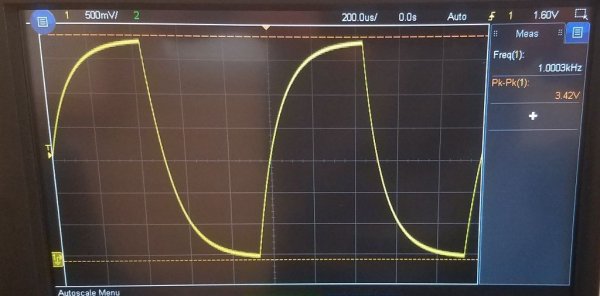
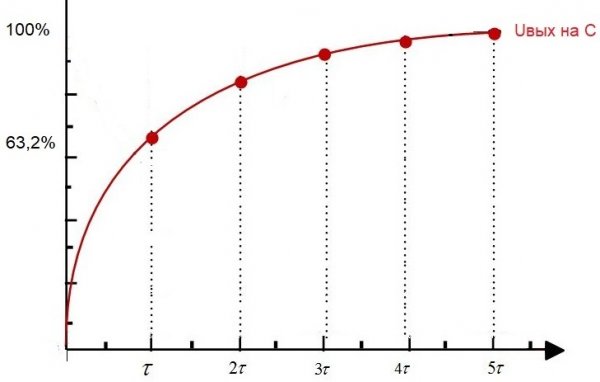
Hvis i det indledende tidspunkt at levere strøm til et sådant kredsløb, det vil sige at indstille en konstant spænding Uin ved indgangen, så vil Uout - spændingen i kondensatoren begynde at vokse eksponentielt.

Efter tiden t1 vil kondensatorspændingen nå 63,2% af indgangsspændingen. Så tidsintervallet fra det indledende øjeblik til t1 er tidskonstanten for dette RC-kredsløb.

Denne kædekonstant kaldes «tau», målt i sekunder og angivet med dets tilsvarende græske bogstav. Numerisk er det for et RC-kredsløb lig med R * C, hvor R er i ohm og C er i farad.

Integrerende RC-kredsløb bruges i elektronik som lavpasfiltre, når højere frekvenser skal afbrydes (undertrykkes) og lavere frekvenser skal passeres igennem.

I praksis er mekanismen for sådan filtrering baseret på følgende princip. For vekselstrøm fungerer kondensatoren som en kapacitiv modstand, hvis værdi er omvendt proportional med frekvensen, det vil sige, jo højere frekvensen er, jo lavere vil kondensatorens reaktans i ohm være.

Derfor, hvis en vekselstrøm føres gennem RC-kredsløbet, vil en vis spænding falde over kondensatoren, som på spændingsdelerens arm, proportionalt med dens kapacitans ved frekvensen af ​​den passerede strøm.

Hvis afskæringsfrekvensen og amplituden af ​​input-vekselsignalet er kendt, vil det ikke være vanskeligt for designeren at vælge en sådan kondensator og modstand i RC-kredsløbet, således at den minimale (cut-off) spænding (for afskæringsfrekvens - den øvre grænse for frekvensen) falder på kondensatoren, da reaktansen kommer ind i deleren sammen med en modstand.

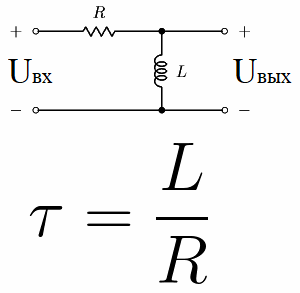
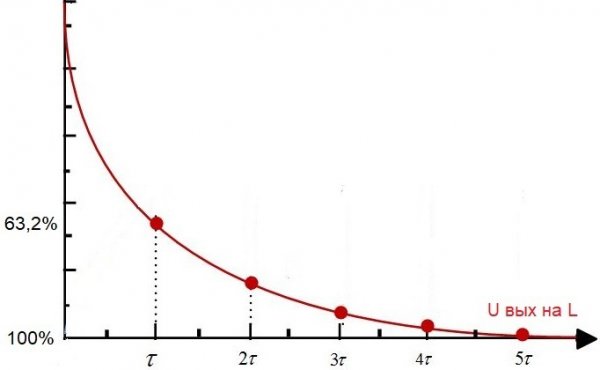
Overvej nu det såkaldte differentieringskredsløb. Det er et kredsløb bestående af en modstand og en induktor forbundet i serie, et RL-kredsløb. Dens tidskonstant er numerisk lig med L / R, hvor L er induktansen af ​​spolen i henries og R er modstanden af ​​modstanden i ohm.

Hvis en konstant spænding fra en kilde påføres et sådant kredsløb, vil spolens spænding efter nogen tid tau falde i forhold til U in med 63,2 %, det vil sige i fuld overensstemmelse med værdien af ​​tidskonstanten for dette elektriske kredsløb .

I AC-kredsløb (vekslende signaler) bruges LR-kredsløb som højpasfiltre, når lave frekvenser skal afbrydes (undertrykkes), og frekvenser over (over afskæringsfrekvensen - den nedre frekvensgrænse) - udelades.Så jo højere induktans af spolen, jo højere frekvens.

Som i tilfældet med RC-kredsløbet beskrevet ovenfor, anvendes spændingsdelerprincippet her. En højere frekvensstrøm passeret gennem RL-kredsløbet vil resultere i et større spændingsfald over induktansen L, som med den induktive modstand, der er en del af spændingsdeleren sammen med modstanden. Designerens opgave er at vælge sådanne R og L, så spolens minimum (grænse)spænding opnås nøjagtigt ved grænsefrekvensen.