Transformer effektivitet

Transformatorens effektivitet bestemmes af forholdet mellem kraften P2 leveret af transformeren og belastningen og effekten P1, der forbruges af netværket:

η = P2/P1

Effektivitet karakteriserer effektiviteten af ​​spændingskonvertering i en transformer.

I praktiske beregninger beregnes transformerens effektivitet ved formlen

η = 1 — (∑P — (P2 + ∑P),

hvor ∑P = Pmail + Pmg — totale tab i transformeren.

Denne formel er mindre følsom over for fejl i bestemmelsen af ​​P1 og P2 og gør det derfor muligt at opnå en mere nøjagtig effektivitetsværdi.

Nettoeffekten, der leveres af transformeren til netværket, beregnes ved hjælp af formlen

P2 = m NS U2n NS I2n NS kng NS Cosφ2 = kng NS Сn NS Cosφ2,

hvor kng = I2 / I2n — belastningsfaktor for transformeren.

De elektriske tab i viklingerne bestemmes af transformatorens kortslutningsoplevelse.

Pmail = kng2 NS PYes,

hvor Pk = rk x I21n — kortslutningstab ved mærkestrøm.

Tab i stål Rmg bestemmes af tomgangstesten rmg = Ro

De antages konstante for alle driftsformer af transformeren, da når u1 = const EMF E1 i driftstilstandene ændres ubetydeligt.

Baseret på ovenstående kan transformatorens effektivitet bestemmes af følgende formel:

η = (Po + kng2 NS PSe) / (kng NS Сn NS Cosφ2 + Po + kng2 NS PSe),

Analyse af dette udtryk viser, at transformatorens virkningsgrad har en maksimal værdi ved belastningen, når tabene i viklingerne er lig dem i stålet.

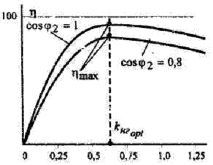
Ris. 1. Bestemmelse af den optimale værdi af transformatorens belastningsfaktor

Fra dette får vi den optimale værdi af transformatorens belastningsfaktor:

kngopt = √Po / PTo være

I moderne krafttransformatorer er tabskoefficienten Po/P1 = (0,25 — 0,4); derfor forekommer maksimum af η ved kng = 0,5 — 0,6 (fig. 1).

Fra η (kng) kurven kan det ses, at transformatoren har næsten konstant virkningsgrad over et bredt belastningsområde fra 0,5 til 1,0. Ved lave belastninger falder transformatorens η kraftigt.

Transformatorstation