RMS værdier af strøm og spænding

Den sinusformede vekselstrøm har forskellige øjeblikkelige værdier i løbet af perioden. Det er naturligt at stille spørgsmålet, hvilken værdi af strøm vil blive målt med amperemeteret inkluderet i kredsløbet?

Ved beregning af vekselstrømkredsløb såvel som elektriske målinger er det ubelejligt at bruge øjeblikkelige eller amplitudeværdier af strømme og spændinger, og deres gennemsnitlige værdier over en periode er nul. Derudover kan den elektriske effekt af en periodisk skiftende strøm (mængden af ​​frigivet varme, den perfekte drift osv.) ikke estimeres ved amplituden af ​​denne strøm.

Det mest bekvemme var introduktionen af ​​begreberne for de såkaldte effektive værdier af strøm og spænding... Disse begreber er baseret på strømmens termiske (eller mekaniske) virkning, som ikke afhænger af dens retning.

Root mean square værdi af vekselstrøm - dette er værdien af ​​jævnstrøm, ved hvilken der i løbet af vekselstrømsperioden frigives den samme mængde varme i lederen som under vekselstrøm.

At evaluere de foranstaltninger, der er truffet vekselstrøm, vil vi sammenligne dens handlinger med den termiske effekt af jævnstrøm.

DC-effekt P A, der passerer gennem modstand r, vil være P = P2r.

Vekselstrøm udtrykkes som den gennemsnitlige effekt af den øjeblikkelige effekt Az2r over hele perioden eller gennemsnittet af (jeg er x sinωT)2 NSr for samme tid.

Lad gennemsnitsværdien af ​​t2 for perioden være M. Ved at sidestille effekten af ​​jævnstrøm og effekt af vekselstrøm, har vi: Az2r = Mr -n, hvorfra Az = √M,

Størrelsen I kaldes den effektive værdi af vekselstrømmen.

Gennemsnitsværdien af ​​i2 ved vekselstrøm bestemmes som følger.

Lad os konstruere en sinusformet strømkurve. Ved at kvadrere hver øjeblikkelig strømværdi får vi en P versus tid-kurve.

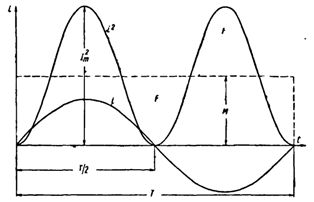AC rms værdi

Begge halvdele af denne kurve ligger over den vandrette akse, da de negative strømme (-i) i anden halvdel af perioden, i kvadrat, giver positive værdier.

Konstruer et rektangel med basis T og areal lig med arealet afgrænset af kurven i2 og vandret akse. Højden af ​​rektanglet M vil svare til gennemsnitsværdien af ​​P for perioden. Denne periodeværdi, beregnet ved hjælp af højere matematik, vil være lig med 1/2 I2m... Derfor er M. = 1/2 I2m

Da rms værdien Im vekselstrøm er Im = √M, så til sidst I = Im / √2

På samme måde har forholdet mellem rms og amplitudeværdierne for spændingen U og E formen:

U = Um / √2E = Em / √2

De effektive værdier af variablerne er angivet med store bogstaver uden underskrift (I, U, E).

Baseret på ovenstående kan vi sige, at den effektive værdi af en vekselstrøm er lig med en sådan jævnstrøm, som, der passerer gennem samme modstand som vekselstrømmen, frigiver den samme mængde energi på samme tid.

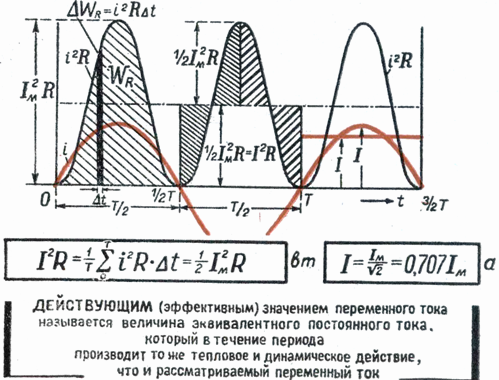
Elektriske måleinstrumenter (amperemeter, voltmetre) inkluderet i et vekselstrømkredsløb angiver de effektive værdier af strøm eller spænding.

Når man konstruerer vektordiagrammer, er det mere bekvemt at udskyde ikke amplituden, men de effektive værdier af vektorerne. Til dette reduceres længderne af vektorerne med √2 én gang. Dette ændrer ikke placeringen af ​​vektorerne på diagrammet.