Potentiale kredsløbsdiagram

Et diagram over potentialet kaldes en grafisk repræsentation af fordelingen af ​​det elektriske potentiale langs en lukket sløjfe, afhængigt af modstanden af ​​sektionerne inkluderet i den valgte sløjfe.

En lukket sløjfe er valgt til at konstruere et potentialdiagram. Dette kredsløb er opdelt i sektioner på en sådan måde, at der er én bruger eller energikilde pr. sektion. Grænsepunkter mellem sektioner skal markeres med bogstaver eller tal.

Et punkt i løkken er vilkårligt jordet, dets potentiale anses betinget for at være nul. Går man rundt om konturen med uret fra et potentiale nul, defineres potentialet for hvert efterfølgende grænsepunkt som den algebraiske sum af potentialet for det foregående punkt og potentialets ændring mellem disse tilstødende punkter.

Ændringen i et objekts potentiale afhænger af sammensætningen af ​​kredsløbet mellem punkterne. Hvis en strømforbruger (modstand) er inkluderet i placeringen, er ændringen i potentiale numerisk lig med spændingsfaldet over den modstand. Tegnet på denne ændring bestemmes af strømmens retning.Hvis løkkens strøm- og bypass-retning stemmer overens, er tegnet negativt, ellers er det positivt.

Hvis der er en EMF-kilde på objektet, så er den potentielle ændring her numerisk lig med EMF-værdien af ​​denne kilde. Hvis løkkens bypassretning og EMF-retningen falder sammen, er den potentielle ændring positiv, ellers er den negativ.

Efter at have beregnet potentialerne for alle punkter, opbygges et potentialediagram i et rektangulært koordinatsystem. På abscisseaksen tegnes sektionernes modstand i skala i den rækkefølge, de mødes i, når de krydser konturen, og på ordinaten de tilsvarende punkters potentialer. Potentialediagrammet starter ved nul potentiale og slutter efter at have cyklet igennem det.

Konstruer et potentialekredsløbsdiagram

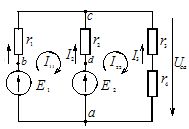
I dette eksempel konstruerer vi et potentialediagram for den første sløjfe af kredsløbet, hvis diagram er vist i figur 1.

Ris. 1. Diagram over et komplekst elektrisk kredsløb

Det betragtede kredsløb omfatter to strømforsyninger E1 og E2 samt to strømforbrugere r1, r2.

Vi opdeler denne kontur i sektioner, hvis grænser er angivet med bogstaverne a, b, c, d. Vi jorder punkt a, konventionelt betragter dets potentiale som nul, og cirkler konturen med uret fra dette punkt. Derfor er φα = 0.

Det næste punkt på stien for at krydse konturen vil være punkt b. EMF-kilden E1 er placeret i afsnit ab. Når vi bevæger os fra den negative til den positive pol af kilden i dette afsnit, stiger potentialet med værdien E1:

φb = φa + E1 = 0 + 24 = 24 V

Når man bevæger sig fra punkt b til punkt c, falder potentialet med størrelsen af ​​spændingsfaldet over modstanden r1 (bypassretningen af ​​sløjfen falder sammen med retningen af ​​strømmen i modstanden r1):

φc = φb — Az1r1 = 24 — 3 x 4 = 12V

Når du går til punkt d, stiger potentialet med mængden af ​​spændingsfald over modstanden r2 (i dette afsnit er strømretningen modsat retningen af ​​sløjfebypasset):

φd = φ° C + I2r2 = 12 + 0 NS 4 = 12 V

Potentialet for punkt a er mindre end potentialet for punkt d med værdien af ​​EMF af kilden E2 (retningen af ​​EMF er modsat retningen for at omgå kredsløbet):

φa = φd — E2 = 12 — 12 = 0

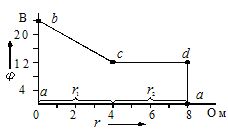
Resultaterne af beregningerne bruges til at bygge et potentialediagram. På abscisseaksen er sektionernes modstand plottet i serie, som det ville være, når kredsløbet er omgivet af et nulpotentiale. De tidligere beregnede potentialer af de tilsvarende punkter er plottet langs ordinaten (fig. 2).

Tegning 2... Potentialkonturdiagram

Patskevich V.A.