Hvordan man beregner induktans

Ligesom et legeme med masse i mekanik modstår acceleration i rummet, der manifesterer inerti, således forhindrer induktans strømmen i en leder i at ændre sig, hvilket manifesterer selvinduktion EMF. Dette er selvinduktionens EMF, som modsætter sig både et fald i strømmen, der forsøger at opretholde den, og en stigning i strømmen, der forsøger at mindske den.

Faktum er, at i processen med at ændre (øge eller mindske) strømmen i kredsløbet, ændres den magnetiske flux, der skabes af denne strøm, også, hvilket hovedsageligt er lokaliseret i det område, der er begrænset af dette kredsløb. Og efterhånden som den magnetiske flux stiger eller falder, inducerer den en EMF af selvinduktion (ifølge Lenz's regel - mod årsagen, der forårsager det, det vil sige mod strømmen nævnt i begyndelsen), alt sammen i det samme kredsløb. Induktansen L her kaldes proportionalitetsfaktoren mellem strømmen I og den totale magnetiske flux Φ, denne strøm genereret af:

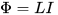
Så jo højere induktans af kredsløbet, jo stærkere er det end det resulterende magnetfelt, det forhindrer strømmen i at ændre sig (det er feltet, der skaber det), og derfor vil det tage længere tid for strømmen at ændre sig gennem større induktans, med samme påførte spænding. Følgende udsagn er også sandt: Jo højere induktans, jo større vil spændingen være over kredsløbet, når den magnetiske flux gennem det ændres.

Antag, at vi ændrer den magnetiske flux i et bestemt område med en konstant hastighed, så ved at dække dette område med forskellige kredsløb, vil vi få mere spænding på det kredsløb, hvis induktans er større (transformator, Rumkorf-spole osv. fungerer efter dette princip).

Men hvordan beregnes sløjfeinduktansen? Hvordan finder man proportionalitetsfaktoren mellem strøm og magnetisk flux? Den første ting at huske er, at induktansen ændrer sig i Henry (H). Ved terminalerne af et kredsløb med en induktans på 1 henry, hvis strømmen i den ændres med en ampere i sekundet, vises en spænding på 1 volt.

Størrelsen af ​​induktansen afhænger af to parametre: af kredsløbets geometriske dimensioner (længde, bredde, antal vindinger osv.) og af mediets magnetiske egenskaber (hvis der f.eks. er en ferritkerne inde i spole, vil dens induktans være større, end hvis der ikke er nogen kerne indeni).

For at beregne den producerede induktans er det nødvendigt at vide, hvilken form selve spolen vil have, og hvilken magnetisk permeabilitet mediet inde i den vil have (mediets relative magnetiske permeabilitet er proportionalitetsfaktoren mellem den magnetiske permeabilitet af et vakuum og den magnetiske permeabilitet af et givet medium.Selvfølgelig er det forskelligt for forskellige materialer) …

Lad os se på formlerne til beregning af induktansen af ​​de mest almindelige former for spoler (cylindrisk solenoide, toroid og lang ledning).

Her er formlen til at beregne induktansen solenoide — spoler, hvis længde er meget større end diameteren:

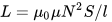
Som du kan se, ved at kende antallet af vindinger N, længden af ​​viklingen l og tværsnitsarealet af spolen S, finder vi den omtrentlige induktans af spolen uden en kerne eller med en kerne, mens den magnetiske permeabiliteten af ​​vakuum er en konstant værdi:

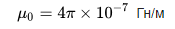
Induktans af en toroidal spole, hvor h er højden af ​​toroid, r er den indre diameter af toroid, R er den ydre diameter af toroid:

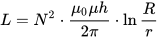
Induktansen af ​​en tynd tråd (tværsnittets radius er meget mindre end længden), hvor l er længden af ​​tråden, og r er radius af dens tværsnit Mu med indeks i og e er relative magnetiske permeabiliteter af de interne (interne, ledermaterialer) og de eksterne (eksterne, materialer uden for lederen) miljøer:

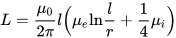
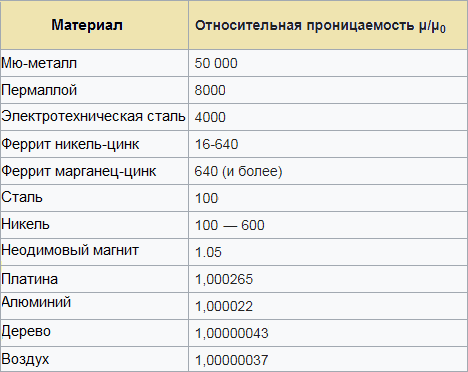
En tabel over relative permittiviteter vil hjælpe dig med at vurdere, hvilken induktans du kan forvente af et kredsløb (tråd, spole) ved hjælp af et bestemt magnetisk materiale som en kerne: