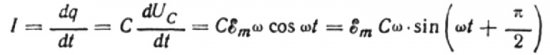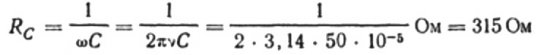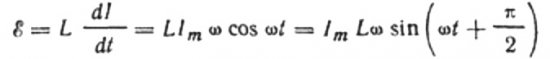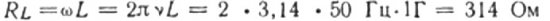Kapacitiv og induktiv modstand i et vekselstrømskredsløb

Hvis vi inddrager en kondensator i et jævnstrømskredsløb, finder vi ud af, at den har uendelig modstand, fordi en jævnstrøm simpelthen ikke kan passere gennem dielektrikumet mellem pladerne, da et dielektrikum per definition ikke leder en jævnstrøm.

En kondensator bryder DC-kredsløbet. Men hvis den samme kondensator nu er inkluderet i vekselstrømskredsløbet, så viser det sig, at dens kondensator ikke ser ud til at gå helt i stykker, den veksler og oplader, det vil sige, den elektriske ladning bevæger sig, og strømmen i det eksterne kredsløb er vedligeholdt.

Baseret på Maxwells teori i dette tilfælde kan vi sige, at vekselledningsstrømmen inde i kondensatoren stadig er lukket, kun i dette tilfælde - af forspændingsstrømmen. Det betyder, at kondensatoren i AC-kredsløbet fungerer som en type modstand med en endelig værdi. Denne modstand kaldes kapacitive.

Praksis har længe vist, at mængden af ​​vekselstrøm, der strømmer gennem en leder, afhænger af lederens form og af de magnetiske egenskaber af mediet omkring den.Med en lige ledning vil strømmen være størst, og hvis den samme ledning vikles ind i en spole med et stort antal vindinger, vil strømmen være mindre.

Og hvis en ferromagnetisk kerne indføres i den samme spole, vil strømmen falde endnu mere. Derfor giver ledningen vekselstrøm ikke kun med en ohmsk (aktiv) modstand, men også med en ekstra modstand, afhængig af ledningens induktans.Denne modstand kaldes induktiv.

Dens fysiske betydning er, at en skiftende strøm i en leder med en vis induktans initierer en EMF af selvinduktion i den leder, som har en tendens til at forhindre ændringer i strømmen, det vil sige har en tendens til at reducere strømmen. Dette svarer til at øge ledningens modstand.

Kapacitans i AC-kredsløbet

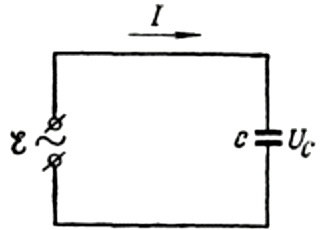
Lad os først tale om kapacitiv modstand mere detaljeret. Antag at en kondensator med kapacitans C er forbundet til en sinusformet vekselstrømkilde, så vil denne kildes EMF blive beskrevet med følgende formel:

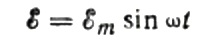
Vi vil ignorere spændingsfaldet over forbindelsesledningerne, da det normalt er meget lille og kan overvejes separat, hvis det er nødvendigt. Lad os nu antage, at spændingen over kondensatorpladerne er lig med AC-kildespændingen. Derefter:

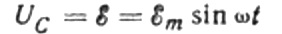
På ethvert givet tidspunkt afhænger ladningen på en kondensator af dens kapacitans og spændingen mellem dens plader. Så, givet den kendte kilde, der blev nævnt ovenfor, får vi et udtryk for at finde ladningen på kondensatorpladerne ved kildespændingen:

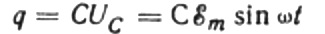
Lad i en uendelig lille tid dt ladningen på kondensatoren ændre sig med dq, så vil en strøm I strømme gennem ledningerne fra kilden til kondensatoren lig med:

Værdien af ​​den aktuelle amplitude vil være lig med:

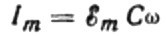
Så vil det endelige udtryk for strømmen være:

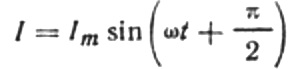
Lad os omskrive den nuværende amplitudeformel som følger:

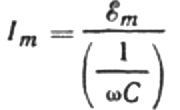
Dette forhold er Ohms lov, hvor det reciproke af produktet af vinkelfrekvens og kapacitans spiller rollen som modstand, og faktisk er et udtryk for at finde kapacitansen af ​​en kondensator i et sinusformet vekselstrømkredsløb:

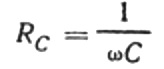
Det betyder, at den kapacitive modstand er omvendt proportional med strømmens vinkelfrekvens og kondensatorens kapacitans. Det er let at forstå den fysiske betydning af denne afhængighed.

Jo større kapacitansen af ​​kondensatoren i AC-kredsløbet og jo oftere retningen af ​​strømmen i det kredsløb ændres, i sidste ende passerer mere total ladning per tidsenhed gennem tværsnittet af ledningerne, der forbinder kondensatoren med AC-kilden. Det betyder, at strømmen er proportional med produktet af kapacitansen og vinkelfrekvensen.

Lad os for eksempel beregne kapacitansen af ​​en kondensator med en elektrisk kapacitet på 10 mikrofarad for et sinusformet vekselstrømkredsløb med en frekvens på 50 Hz:

Hvis frekvensen var 5000 Hz, ville den samme kondensator have en modstand på omkring 3 ohm.

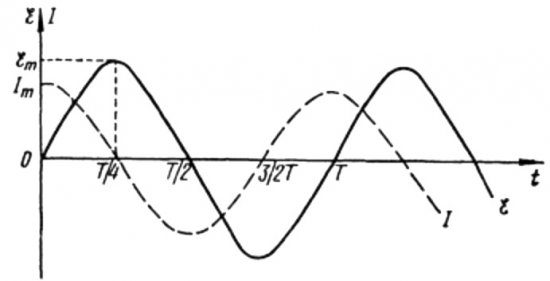
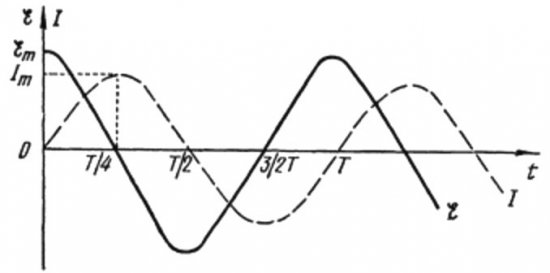
Fra ovenstående formler er det klart, at strømmen og spændingen i et AC-kredsløb med en kondensator altid ændrer sig i forskellige faser. Den aktuelle fase fører spændingsfasen med pi / 2 (90 grader). Det betyder, at den maksimale strøm i tid altid eksisterer en kvart periode tidligere end den maksimale spænding. På tværs af den kapacitive modstand fører strømmen således spændingen en fjerdedel af tidsperioden eller med 90 grader i fase.

Lad os forklare den fysiske betydning af dette fænomen.I det første øjeblik af tid er kondensatoren fuldstændig afladet, så den mindste spænding, der påføres den, flytter allerede ladningerne på kondensatorens plader og skaber en strøm.

Når kondensatoren oplades, stiger spændingen over dens plader, dette forhindrer yderligere ladningsstrøm, så strømmen i kredsløbet falder på trods af yderligere stigninger i spændingen på pladerne.

Det betyder, at hvis strømmen i det indledende tidspunkt var maksimal, så vil strømmen stoppe helt, når spændingen når sit maksimum efter en kvart periode.

I begyndelsen af ​​perioden er strømmen maksimal, og spændingen er minimum og begynder at stige, men efter en fjerdedel af perioden når spændingen et maksimum, men strømmen er allerede faldet til nul på dette tidspunkt. Således viser det sig, at spændingen fører spændingen med en fjerdedel af perioden.

AC induktiv modstand

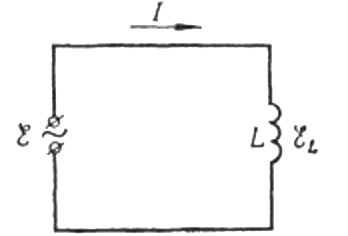
Nu tilbage til induktiv modstand. Antag, at en sinusformet vekselstrøm løber gennem en induktansspole. Det kan udtrykkes som:

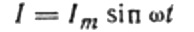
Strømmen skyldes vekselspændingen på spolen. Dette betyder, at en EMF af selvinduktion vil fremkomme på spolen, som udtrykkes som følger:

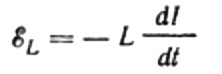
Igen forsømmer vi spændingsfaldet over ledningerne, der forbinder EMF-kilden til spolen. Deres ohmske modstand er meget lav.

Lad den vekselspænding, der påføres spolen på ethvert tidspunkt, være fuldstændig afbalanceret af den opståede EMF af selvinduktion svarende til den i størrelsesorden, men modsat i retning:

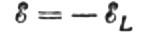
Så har vi ret til at skrive:

Da amplituden af ​​spændingen påført spolen er:

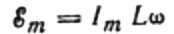
vi får:

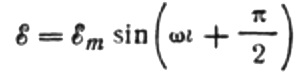
Lad os udtrykke den maksimale strøm som følger:

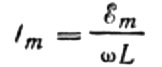
Dette udtryk er grundlæggende Ohms lov. En mængde svarende til produktet af induktansen og vinkelfrekvensen spiller her rollen som modstand og er intet andet end induktorens induktive modstand:

Så den induktive modstand er proportional med spolens induktans og vinkelfrekvensen af ​​vekselstrømmen gennem spolen.

Dette skyldes, at induktiv modstand skyldes selvinduktions-EMFs indflydelse på kildespændingen, - selvinduktions-EMK har en tendens til at reducere strømmen og bringer derfor modstand i kredsløbet. Størrelsen af ​​selvinduktionens emk er som bekendt proportional med spolens induktans og strømmens ændringshastighed gennem den.

Lad os for eksempel beregne den induktive modstand af en spole med en induktans på 1 H, som er inkluderet i et kredsløb med en strømfrekvens på 50 Hz:

Hvis kuglens frekvens var 5000 Hz, ville modstanden af ​​den samme spole være cirka 31.400 ohm. Husk på, at den ohmske modstand af spoleledningen normalt er nogle få ohm.

Ud fra ovenstående formler er det tydeligt, at ændringerne i strømmen gennem spolen og spændingen i den forekommer i forskellige faser, og strømmens fase er altid mindre end spændingens fase ved pi/2. maksimal strøm opstår en kvart periode senere end indtræden af ​​maksimal stress.

I induktiv modstand forsinker strømmen spændingen med 90 grader på grund af bremseeffekten af ​​den selv-inducerede EMF, som forhindrer strømmen i at ændre sig (både stigende og faldende), så den maksimale strøm observeres i kredsløbet med spolen senere end den maksimale spænding.

Spole og kondensator kombineret handling

Hvis man forbinder en spole med en kondensator i serie med et vekselstrømkredsløb, så vil spolespændingen fremskynde kondensatorspændingen tidsmæssigt med en halv periode, det vil sige med 180 grader i fase.

Kapacitiv og induktiv modstand kaldes reaktanter… Energi bliver ikke brugt på reaktiv modstand som i aktiv modstand. Den energi, der er lagret i kondensatoren, returneres periodisk tilbage til kilden, når det elektriske felt i kondensatoren forsvinder.

Det er det samme med en spole: Da spolens magnetfelt skabes af strømmen, akkumuleres energien i den i løbet af en fjerdedel af perioden, og i løbet af den næste fjerdedel af perioden vender den tilbage til kilden. I denne artikel har vi talt om sinusformet vekselstrøm, for hvilken disse regler følges nøje.

I AC sinusformede kredsløb kaldes kerneinduktorer kvælendebruges traditionelt til strømbegrænsning. Deres fordel i forhold til reostater er, at energi ikke spredes i store mængder som varme.