Klassificering af elektriske måleinstrumenter, instrumentskalasymboler

For at kontrollere den korrekte drift af elektriske installationer, teste dem, bestemme parametrene for elektriske kredsløb, registrere den forbrugte elektriske energi osv., udføres forskellige elektriske målinger. I kommunikationsteknologi, som i moderne teknologi, er elektriske målinger afgørende. De enheder, som forskellige elektriske størrelser måles med: strøm, spænding, modstand, effekt osv., kaldes elektriske måleinstrumenter.

Panel amperemeter:

Der findes et stort antal forskellige elmålere. Følgende bruges oftest i produktionen af ​​elektriske målinger: amperemetre, voltmetre, galvanometre, wattmetre, elektriske måleapparater, fasemålere, faseindikatorer, synkroskoper, frekvensmålere, ohmmetre, megohmmetre, jordmodstande, kapacitans- og induktansmålere, oscilloskoper, målebroer, kombinationsværktøjer og målesæt.

Oscilloskop:

Elektrisk målesæt K540 (inkluderer voltmeter, amperemeter og wattmeter):

Klassificering af elektriske værktøjer i henhold til driftsprincippet

I henhold til driftsprincippet er elektriske måleanordninger opdelt i følgende hovedtyper:

1. Enheder i det magnetoelektriske system baseret på princippet om vekselvirkning af spolen med en strøm og et eksternt magnetfelt skabt af en permanent magnet.

2. NStools til et elektrodynamisk system baseret på princippet om elektrodynamisk interaktion mellem to spoler med strømme, hvoraf den ene er stationær og den anden er bevægelig.

3. Enheder af det elektromagnetiske system, hvor princippet om interaktion af magnetfeltet i en stationær spole med en strøm og en bevægelig jernplade magnetiseret af dette felt anvendes.

4. Termomåleapparater, der anvender den termiske effekt af elektrisk strøm. Tråden, der opvarmes af strømmen, strækker sig, hænger ned, og som et resultat kan den bevægelige del af enheden roteres under påvirkning af fjederen, hvilket fjerner den resulterende slæk i tråden.

5. Enheder af induktionssystemet, baseret på princippet om interaktion af et roterende magnetfelt med strømme induceret af dette felt i en bevægelig metalcylinder.

6. Elektrostatiske systemanordninger baseret på princippet om samspil mellem bevægelige og ubevægelige metalplader ladet med modsatte elektriske ladninger.

7. Termoelektriske systemenheder, som er en kombination af et termoelement med en eller anden følsom enhed, såsom et magnetoelektrisk system. Den målte strøm, der passerer gennem termoelementet, bidrager til udseendet af en termisk strøm, der virker på den magnetoelektriske enhed.

8.Vibrationssystemenheder baseret på princippet om mekanisk resonans af vibrerende legemer. Ved en given strømfrekvens vibrerer et af elektromagnetens armaturer mest intensivt, hvis periode med naturlige svingninger falder sammen med perioden med pålagte svingninger.

9. Elektroniske måleapparater - apparater, hvis målekredsløb indeholder elektroniske komponenter. De bruges til at måle næsten alle elektriske størrelser, såvel som ikke-elektriske størrelser, der er blevet omdannet til elektriske.

Afhængigt af typen af ​​læseenhed skelnes der mellem analoge og digitale enheder. I analoge instrumenter påvirker den målte eller proportionale værdi direkte positionen af ​​den bevægelige del, hvorpå læseapparatet er placeret. I digitale enheder er den bevægelige del fraværende, og den målte eller proportionale værdi konverteres til en numerisk ækvivalent optaget med en digital indikator.

Induktionsmåler:

Afbøjningen af ​​den bevægelige del i de fleste elektriske målemekanismer afhænger af værdierne af strømmene i deres viklinger. Men i tilfælde, hvor mekanismen skal tjene til at måle en størrelse, der ikke er en direkte funktion af strømmen (modstand, induktans, kapacitans, faseforskydning, frekvens osv.), er det nødvendigt, at det resulterende drejningsmoment afhænger af den målte mængde og uafhængig af forsyningsspænding.

Til sådanne målinger bruges en mekanisme, hvis afvigelse af den bevægelige del kun bestemmes af forholdet mellem strømmene i dens to viklinger og ikke afhænger af deres værdier. Enheder bygget efter dette generelle princip kaldes forhold.Det er muligt at konstruere en ratiometrisk mekanisme for ethvert elektrisk målesystem med et karakteristisk træk - fraværet af et mekanisk modvirkende moment skabt af torsion af fjedre eller striae.

Voltmeter forklaring:

Nedenstående figurer viser symbolerne for elektriske målere i henhold til deres funktionsprincip.

Bestemmelse af princippet om enhedens drift

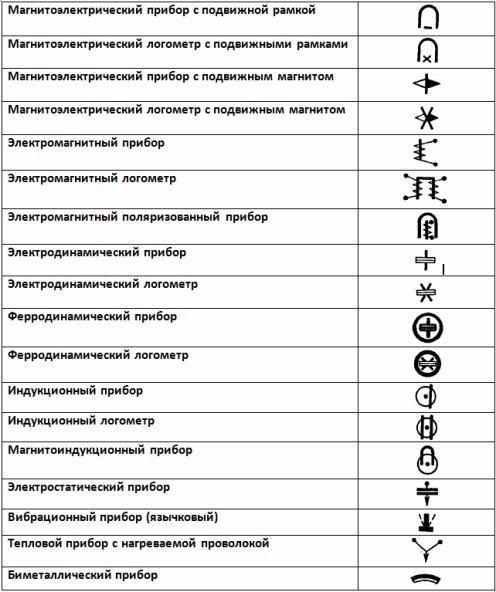
Aktuelle typebetegnelser

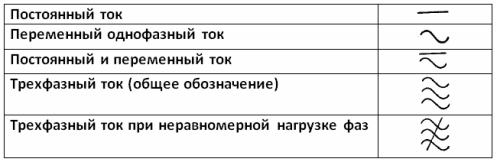
Betegnelser for nøjagtighedsklasse, enhedsposition, isoleringsstyrke, påvirkningsmængder

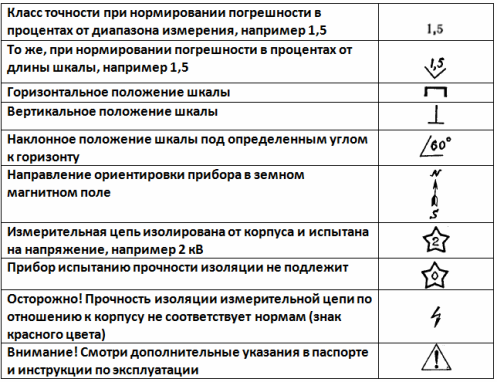
Klassificering af elektriske måleapparater efter typen af ​​målt størrelse

Elektriske målere klassificeres også efter arten af ​​den mængde, de måler, da instrumenter med samme funktionsprincip, men designet til at måle forskellige mængder, kan afvige meget fra hinanden i deres konstruktion, for ikke at nævne skalaen på enheden.

Tabel 1 viser en liste over symboler for de mest almindelige elmålere.

Tabel 1. Eksempler på betegnelse af måleenheder, deres multipla og delmængder

Navn Betegnelse Navn Betegnelse Kiloampere kA Effektfaktor cos φ Ampere A Reaktiv effektfaktor sin φ Milliampere mA Theraohm TΩ Mikroampere μA Megaohm MΩ Kilovolt kV Kilohm kΩ Volt V Ohm Ω Millivolt mV Milliohm mΩ Milliohm mΩ Megawatt MW Mikrob m Megawatt MW Micro var MVAR Picofarad pF Kilovar kVAR Henry H Var VAR Milhenry mH Megahertz MHz Mikrohenry µH KHz kHz Temperaturskala grader Celsius o° C Hertz Hz

Grad af fasevinklen φo

Klassificering af elektriske måleinstrumenter efter graden af ​​nøjagtighed

Enhedens absolutte fejl er forskellen mellem aflæsningen af ​​enheden og den sande værdi af den målte værdi.

For eksempel er den absolutte fejl på amperemeteret

δ = I — aiH,

hvor δ (læs "delta") - absolut fejl i ampere, Az - måleraflæsning i ampere, Azd - den sande værdi af den målte strøm i ampere.

Hvis I > Azd, så er enhedens absolutte fejl positiv, og hvis I < I, er den negativ.

En enhedskorrektion er en værdi, der skal lægges til enhedsaflæsningen for at opnå den sande værdi af den målte værdi.

Aze = I — δ = I + (-δ)

Derfor er korrektionen af ​​enheden værdien af ​​enhedens rabsolute absolutte fejl, men modsat den i fortegn. For eksempel, hvis amperemeteret viser 1 = 5 A, og enhedens absolutte fejl er δ= 0,1 a, så er den sande værdi af den målte værdi I = 5+ (-0,1) = 4,9 a.

Enhedens reducerede fejl er forholdet mellem den absolutte fejl og den størst mulige afvigelse af enhedsindikatoren (nominel aflæsning af enheden).

For eksempel til et amperemeter

β = (δ / In) 100 % = ((I — INS) / In) 100 %

hvor β — reduceret fejl i procent, In er den nominelle aflæsning af instrumentet.

Enhedens nøjagtighed er karakteriseret ved værdien af ​​dens maksimale reducerede fejl. Ifølge GOST 8.401-80 er enheder opdelt i 9 i henhold til graden af ​​deres nøjagtighedsklasser: 0,02, 0,05, 0,1, 0,2, 0,5, 1,0, 1,5, 2,5 og 4 ,0. For eksempel, hvis denne enhed har en nøjagtighedsklasse på 1,5, betyder det, at dens maksimale reducerede fejl er 1,5 %.

Elmålere med nøjagtighedsklasserne 0,02, 0,05, 0,1 og 0,2, som de mest nøjagtige, anvendes, hvor der kræves meget høj målenøjagtighed. Hvis enheden har en reduceret fejl på mere end 4 %, anses den for at være uden for klasse.

Fasevinkelmåleinstrument med nøjagtighedsklasse 2.5:

Følsomhed og konstant for måleapparatet

Enhedens følsomhed er forholdet mellem den vinkelmæssige eller lineære bevægelse af enhedens viser pr. enhed af den målte værdi.Hvis enhedens skala er den samme, så er dens følsomhed over hele skalaen den samme.

For eksempel bestemmes følsomheden af ​​et amperemeter med samme skala af formlen

S = Δα / ΔI,

hvor C — amperemeterfølsomhed i amperedelinger, ΔAz — strømstigning i ampere eller milliampere, Δα — stigning i vinkelforskydning af enhedsindikatoren i grader eller millimeter.

Hvis enhedens skala er ujævn, er enhedens følsomhed i forskellige områder af skalaen forskellig, da den samme stigning (for eksempel strøm) vil svare til forskellige trin af den vinkelmæssige eller lineære forskydning af indikatoren for en instrument.

Instrumentets gensidige følsomhed kaldes instrumentkonstanten. Enhedskonstanten er derfor enhedsprisen for enheden, eller med andre ord den værdi, som skalaaflæsningen i divisioner skal ganges med for at opnå den målte værdi.

For eksempel, hvis konstanten for enheden er 10 mA / div (ti milliampere pr. division), så når dens pointer afviger fra α = 10 divisioner, er den målte strømværdi I = 10 · 10 = 100 mA.

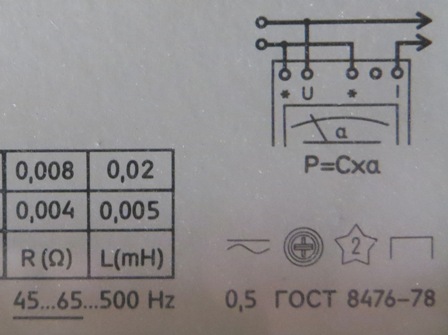
Wattmåler:

Wattmeter tilslutningsdiagram og betegnelser for enheden (ferrodynamisk enhed til måling af variabel og konstant effekt med en vandret position af skalaen, målekredsløbet er isoleret fra kabinettet, og den testede spænding er 2 kV, nøjagtighedsklasse er 0,5):

Kalibrering af måleinstrumenter - bestemmelse af fejl eller korrektioner for et sæt skalaværdier af et instrument ved at sammenligne forskellige kombinationer af individuelle skalaværdier med hinanden. Sammenligningen er baseret på en af ​​skalaværdierne.Kalibrering er meget udbredt i praksis med præcisionsmetrologisk arbejde.

Den enkleste måde at kalibrere på er at sammenligne hver størrelse med en nominelt ens (rimeligt korrekt) størrelse. Dette koncept bør ikke forveksles (som det ofte gøres) med gradueringen (kalibreringen) af måleinstrumenter, som er en metrologisk operation, hvorved måleinstrumentets skalainddelinger gives værdier udtrykt i bestemte måleenheder.

Strømtab i enheder

Elektriske måleapparater bruger energi under drift, som normalt omdannes til varmeenergi. Strømtab afhænger af tilstanden i kredsløbet samt systemet og enhedens design.

Hvis den målte effekt er relativt lille, og derfor er strømmen eller spændingen i kredsløbet relativt lille, kan energitabet i selve enhederne betydeligt påvirke tilstanden af ​​det kredsløb, der undersøges, og enhedernes aflæsninger kan have en ret stor fejl. For nøjagtige målinger i kredsløb, hvor de udviklede kræfter er relativt små, er det nødvendigt at kende styrken af ​​energitabene i enhederne.

Tabel 2 viser gennemsnitsværdierne for energieffekttab i forskellige elmålersystemer.

Instrumenteringssystem Voltmetre 100 V, W Amperemeter 5A, W Magnetoelektrisk 0,1 — 1,0 0,2 — 0,4 Elektromagnetisk 2,0 — 5,0 2,0 — 8,0 Induktion 2,0 — 5,0 1 ,0 — 4,0 Elektrodynamisk 6 003 — 0,03 — 5,03 — 0. 0 2,0 - 3,0