Linearisering af sensorkarakteristika

Linearisering af sensorkarakteristika — en ikke-lineær transformation af sensoroutputværdien eller en mængde, der er proportional med den (analog eller digital), der opnår et lineært forhold mellem den målte værdi og den værdi, der repræsenterer den.

Ved hjælp af linearisering er det muligt at opnå linearitet på skalaen af ​​den sekundære enhed, hvortil en sensor med en ikke-lineær karakteristik er forbundet (f.eks. termoelement, termisk modstand, gasanalysator, flowmåler osv.). Lineariseringen af ​​sensoregenskaberne gør det muligt at opnå den nødvendige målenøjagtighed gennem sekundære enheder med digital udgang. Dette er nødvendigt i nogle tilfælde ved tilslutning af sensorer til registreringsenheder eller ved udførelse af matematiske operationer på den målte værdi (f.eks. integration).

Med hensyn til indkoderkarakteristikken virker lineariseringen som en omvendt funktionel transformation.Hvis karakteristikken for sensoren er repræsenteret som y = F (a + bx), hvor x er den målte værdi, a og b er konstanter, så skal karakteristikken for linearisatoren forbundet i serie med sensoren (fig. 1) se ud. sådan: z = kF (y), hvor F er den omvendte funktion af F.

Som et resultat vil outputtet af linearisatoren være z = kF(F (a + bx)) = a ' + b'x, dvs. en lineær funktion af den målte værdi.

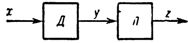
Ris. 1. Generaliseret lineariseringsblokdiagram: D — sensor, L — linearisator.

Endvidere reduceres afhængigheden z ved skalering til formen z '= mx, hvor m er den passende skalafaktor. Hvis lineariseringen udføres på en kompensatorisk måde, dvs. baseret på et servosystem som fig. 2, så skal karakteristikken for lineariseringsfunktionsomformeren svare til karakteristikken for sensoren z = cF (a + bx), fordi den lineariserede værdi af den målte værdi er taget fra input fra konverteren til funktionslinearisatoren og dens output sammenlignes med udgangsværdien af ​​sensoren.

Et karakteristisk træk ved linearisatorer som funktionelle konvertere er en relativt snæver klasse af afhængigheder gengivet af dem, begrænset til monotone funktioner, som bestemmes af typen af ​​sensorkarakteristika.

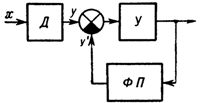
Ris. 2. Blokdiagram over linearisering baseret på sporingssystemet: D — sensor, U — forstærker (transducer), FP — funktionel konverter.

Linearisatorer kan klassificeres efter følgende kriterier:

1. Ifølge metoden til indstilling af funktionen: rumlig i form af skabeloner, matricer osv., i form af en kombination af ikke-lineære elementer, i form af en digital beregningsalgoritme, enheder.

2.Ved graden af ​​fleksibilitet af ordningen: universel (dvs. rekonfigurerbar) og specialiseret.

3. I henhold til strukturdiagrammets art: åben (fig. 1) og kompensation (fig. 2) type.

4. I form af input- og outputværdier: analog, digital, blandet (analog-digital og digital-analog).

5. Efter type af elementer, der anvendes i kredsløbet: mekaniske, elektromekaniske, magnetiske, elektroniske osv.

Rumlige funktionslinearisatorer omfatter primært knastmekanismer, mønstre og ikke-lineære potentiometre. De bruges i tilfælde, hvor den målte værdi af hvert konverteringstrin præsenteres i form af mekanisk bevægelse (knaster - til linearisering af karakteristika for manometriske sensorer og transformersensorer, modeller - i optagere, ikke-lineære potentiometre - i potentiale- og brokredsløb ).

Potentiometeregenskabernes ulinearitet opnås ved opvikling på profilerede rammer og sektionering ved hjælp af den stykkevise lineære tilnærmelsesmetode ved at manøvrere sektionerne med passende modstande.

I en linearisator baseret på et elektromekanisk servosystem af potentiometrisk type, der anvender et ikke-lineært potentiometer (fig. 3), vises den lineariserede værdi som en rotationsvinkel eller mekanisk forskydning. Disse linearisatorer er enkle, alsidige og udbredt i centraliserede kontrolsystemer.

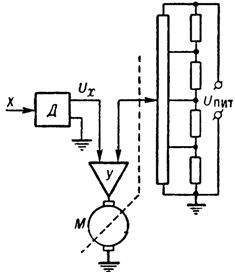
Ris. 3. Linearizer til elektromekanisk servosystem af potentiometrisk type: D — sensor med udgang i form af DC-spænding, Y — forstærker, M — elektrisk motor.

Ikke-lineariteter af individuelle elementers egenskaber (elektroniske, magnetiske, termiske osv.) bruges i parametriske funktionelle omformere. Men mellem de funktionelle afhængigheder, de udvikler, og sensorernes egenskaber, er det normalt ikke muligt at opnå et fuldstændigt match.

Den algoritmiske måde at indstille en funktion på bruges i digitale funktionskonvertere. Deres fordele er høj nøjagtighed og stabilitet af egenskaber. De bruger de matematiske egenskaber ved individuelle funktionelle afhængigheder eller princippet om lineær tilnærmelse af dele. For eksempel udvikles en parabel baseret på egenskaberne for kvadrater af heltal.

For eksempel er en digital linearizer baseret på den stykkevise lineære approksimationsmetode, som fungerer efter princippet om at fylde de nærgående segmenter med impulser med forskellige gentagelseshastigheder. Fyldningsfrekvenserne ændrer sig i hop ved grænsepunkterne for de nærgående segmenter i henhold til det program, der er indsat i enheden i henhold til typen af ​​ikke-linearitet. Den lineariserede mængde konverteres derefter til en enhedskode.

En delvis lineær tilnærmelse af ikke-lineariteten kan også udføres ved hjælp af en digital lineær interpolator. I dette tilfælde forbliver fyldningsfrekvenserne af interpolationsintervallerne kun konstante i gennemsnit.

Fordelene ved digitale linearizere baseret på metoden til lineær tilnærmelse af dele er: nem rekonfiguration af den akkumulerede ikke-linearitet og hastigheden af ​​at skifte fra en ikke-linearitet til en anden, hvilket er særligt vigtigt i højhastighedscentraliserede kontrolsystemer.

I komplekse styresystemer, der indeholder universelle regnemaskiner, maskiner, kan linearisering udføres direkte fra disse maskiner, hvor funktionen er indlejret i form af en tilsvarende subrutine.