Logiske enheder

Logisk algebra eller boolsk algebra bruges til at beskrive funktionslovene for digitale kredsløb. Logikkens algebra er baseret på konceptet om en "begivenhed", der kan eller ikke kan ske. En hændelse, der har fundet sted, betragtes som sand, og et logisk niveau «1» er udtrykt, en hændelse, der ikke er indtruffet, betragtes som falsk, og et logisk niveau «0» er udtrykt.

Hændelsen er påvirket af variabler, og de påvirker i henhold til en bestemt lov. Denne lov kaldes en logisk funktion, variablerne er argumenter... Che. den logiske funktion er funktionen y = f (x1, x2, … xn), som tager værdierne «0» eller «1». Variablerne x1, x2, … xn har også værdierne «0» eller «1».

Algebra of logic - en gren af ​​matematisk logik, der studerer strukturen af ​​komplekse logiske udsagn og måder at fastslå deres sandhed ved hjælp af algebraiske metoder. I formlerne for logisk algebra er variablerne logiske eller binære, det vil sige, at de kun tager to værdier - falsk og sand, som er angivet med henholdsvis 0 og 1. Hvert computerprogram indeholder logiske operationer.

Enheder designet til at danne funktioner i den logiske algebra kaldes logiske enheder... En logisk enhed har et vilkårligt antal indgange og kun én udgang (fig. 1).

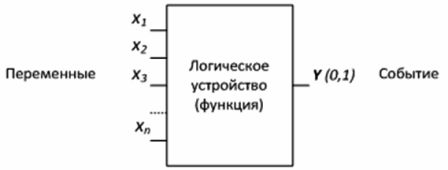
Figur 1 — Logisk enhed

For eksempel indbefatter en elektronisk kombinationslås en logisk anordning, for hvilken hændelse (y) er åbningen af ​​låsen. For at hændelsen (y = 1) skal forekomme, dvs. låsen er åbnet, er det nødvendigt at definere variablerne — ti knapper på det numeriske tastatur. Visse knapper skal trykkes, dvs. tag værdien «1» og tryk samtidig i en bestemt rækkefølge — en logisk funktion.

Det er praktisk at repræsentere enhver logisk funktion i form af en tilstandstabel (sandhedstabel), hvor mulige kombinationer af variable (argumenter) og den tilsvarende værdi af funktionen er registreret.

Logiske enheder er bygget på logiske porte, der udfører en bestemt funktion. De grundlæggende logiske funktioner er logisk addition, logisk multiplikation og logisk negation.

1) ELLER (ELLER) — logisk addition eller division (fra engelsk disjunktion — interruption) — en logisk enhed vises ved udgangen af ​​dette element, når en enhed optræder ved mindst en af ​​indgangene. Udgangen vil kun være logisk nul, når der er et logisk nulsignal på alle indgange.

Denne operation kan udføres ved hjælp af et kontaktkredsløb med to kontakter forbundet parallelt. «1» ved udgangen af ​​et sådant kredsløb vises, hvis mindst en af ​​kontakterne er lukket.

2) OG (AND) — logisk multiplikation eller forbindelse (fra den engelske union — forbindelse, & — og-tegn) — ved udgangen af ​​dette element vises signalet fra en logisk enhed kun, når en logisk enhed er til stede ved alle indgange.Hvis mindst én indgang er nul, vil udgangen også være nul.

Denne operation kan udføres af et kontaktkredsløb bestående af kontakter forbundet i serie.

3) NOT – logisk negation eller inversion angivet med en tankestreg over en variabel – operationen udføres på én variabel x og værdien af ​​y er den modsatte af denne variabel.

Operationen kan IKKE udføres med en normalt lukket kontakt på det elektromagnetiske relæ: der er ingen spænding på relæspolen (x = 0) — kontakten er også lukket ved udgangen «1» (y = 1). Ved tilstedeværelse af spænding på relæspolen (x = 1), er kontakten også åben på «0»-udgangen (y = 0).

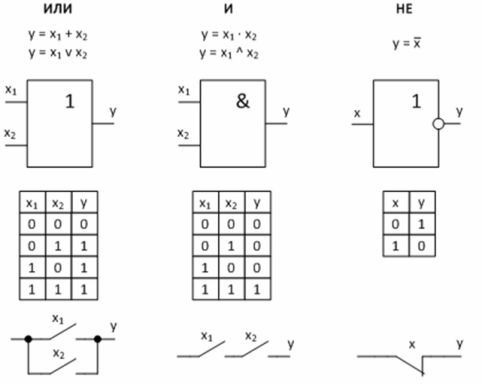
Figur 2 — Grundlæggende logiske funktioner og deres implementering

Logiske enheder bruger forskellige logiske porte. Særligt vigtige er to universelle logiske operationer, som hver især er i stand til uafhængigt at danne enhver logisk funktion.

4) NAND — Schäfer funktion.

5) ELLER IKKE — Punch-funktion.

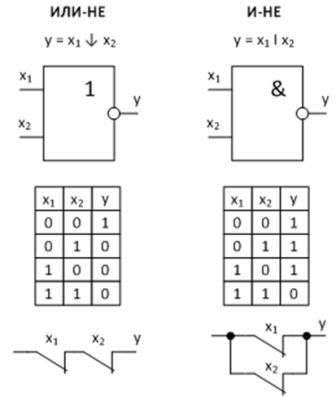
Figur 3 — Universelle logiske funktioner og deres implementering

Eksempel: Sikkerhedsalarmkredsløb baseret på logiske elementer. Generator G genererer et sirenesignal, der fører det til forstærkertrinnet gennem det logiske element «AND» på mikrokredsløbet DD2. Når beskyttelseskontakterne S1 — S4 er lukkede, virker niveauet «0» på indgangene til elementet DD1 — niveauet «0» er på den nedre indgang af elementet «I» DD2, hvilket betyder, at transistorens gate VT er også «0».

I tilfælde af åbning af mindst en af ​​kontakterne, for eksempel S1, vil indgangen til elementet DD1 gennem modstanden R1 modtage en spænding på niveau «1», hvilket vil forårsage udseendet af «1» ved den anden indgang af elementet «OG» DD1.Dette vil tillade signalet fra generatoren G at passere til porten på transistoren, hvis belastning er højttaleren.

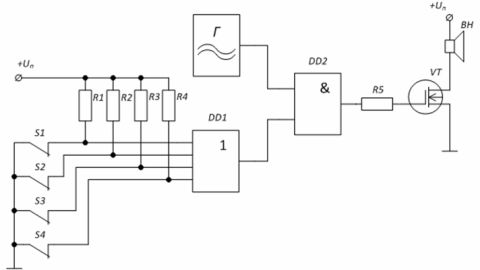
Figur 4 — Alarmbeskyttelsesskema

Komplekse digitale kredsløb er bygget ved at gentage grundlæggende logiske kredsløb igen og igen. Værktøjet til en sådan konstruktion er boolsk algebra, som med hensyn til digital teknologi kaldes logisk algebra. I modsætning til en variabel i almindelig algebra har en boolsk variabel kun to værdier, som kaldes boolsk nul og boolsk en.

Logisk nul og logisk et er betegnet med 0 og 1. I logisk algebra er 0 og 1 ikke tal, men logiske variable. I logisk algebra er der tre grundlæggende operationer mellem logiske variable: logisk multiplikation (konjunktion), logisk addition (disjunktion) og logisk negation (inversion).

Elektroniske kredsløb, der udfører den samme logiske funktion, men samlet med forskellige elementer, der adskiller sig i strømforbrug, forsyningsspænding, værdier af høje og lave udgangsspændingsniveauer, signaludbredelsesforsinkelse og belastningskapacitet.

Se også om dette emne: AND, OR, NOT, AND-NOT, OR-NOT logiske porte og deres sandhedstabeller