Parallel magnetiseringsmotorbremsetilstande

Motorbremsetilstanden i det elektriske drev bruges sammen med motoren. Brugen af ​​en elmotor som elektrisk bremse er i praksis meget udbredt til at forkorte stop- og kørselstiden, reducere omdrejningshastigheden, forhindre den for store stigning i kørehastigheden og i en række andre tilfælde.

Driften af ​​den elektriske motor som en elektrisk bremse er baseret på princippet om reversibilitet af elektriske maskiner, det vil sige, at den elektriske motor under visse forhold skifter til generatortilstand.

I praksis bruges tre tilstande til bremsning:

1) generator (regenerativ) med energiretur til nettet,

2) elektrodynamisk,

3) modstand.

Når man konstruerer mekaniske egenskaber i et rektangulært koordinatsystem, er det vigtigt at bestemme tegnene på motorens drejningsmoment og rotationshastighed i motor- og bremsetilstandene. Til dette tages motortilstanden normalt som den vigtigste, idet motorens omdrejningshastighed og drejningsmoment i denne tilstand betragtes som positiv.I denne henseende er karakteristika n = f (M) for motortilstanden placeret i den første kvadrant (fig. 1). Placeringen af ​​de mekaniske egenskaber i bremsetilstandene afhænger af tegnene på drejningsmomentet og rotationshastigheden.

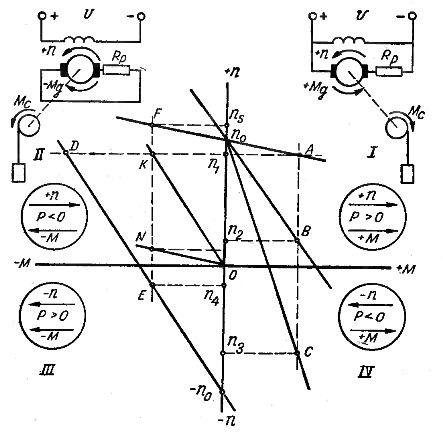
Ris. 1... Tilslutningsdiagrammer og mekaniske karakteristika for en parallel-exciteret motor i motor- og bremsetilstande.

Lad os overveje disse tilstande og de tilsvarende sektioner af parallel-excitationsmotorens mekaniske egenskaber.

Modstand.

Det elektriske drevs tilstand bestemmes af den kombinerede virkning af motordrejningsmomentet Md og det statiske belastningsmoment Mc. For eksempel, steady-state rotationshastigheden n1, når en last løftes med et spil, svarer den til motorens drift i en naturlig karakteristik (Fig.1 punkt A), når Md = Ms. Hvis der indføres yderligere modstand i motorens ankerkredsløb, vil rotationshastigheden falde på grund af overgangen til rheostatkarakteristikken (punkt B svarende til hastighed n2 og Md = Ms).

En yderligere gradvis stigning i den ekstra modstand i motorens ankerkredsløb (for eksempel til en værdi svarende til sektionen n0Karakteristika C) vil først føre til, at løftningen af ​​lasten ophører, og derefter til en ændring i omdrejningsretningen , det vil sige, at lasten falder (punkt C). Et sådant regime kaldes opposition.

I den modsatte tilstand har øjeblikket Md et positivt fortegn. Tegnet på omdrejningshastigheden ændrede sig og blev negativt. Derfor findes de mekaniske karakteristika for oppositionstilstanden i fjerde kvadrant, og selve tilstanden er generativ.Dette følger af den accepterede betingelse for bestemmelse af tegn på drejningsmoment og omdrejningstal.

Faktisk er den mekaniske effekt proportional med produktet n og M, i motortilstand har den et positivt fortegn og ledes fra motoren til arbejdsmaskinen. I oppositionstilstanden, på grund af det negative tegn på n og det positive tegn på M, vil deres produkt være negativt, derfor overføres mekanisk kraft i den modsatte retning - fra arbejdsmaskinen til motoren (generatortilstand). I fig. 1 tegn n og M i motor- og bremsetilstande er vist i cirkler, pile.

De sektioner af den mekaniske karakteristik, der svarer til den oppositionelle tilstand, er en naturlig forlængelse af motortilstandens karakteristika fra den første til den fjerde kvadrant.

Fra det overvejede eksempel på at skifte motoren til den modsatte tilstand, kan det ses, at f.eks. etc. c. motoren, afhængigt af omdrejningshastigheden, samtidig med den sidste, når den krydser nulværdien, ændrer fortegn og virker i overensstemmelse med netspændingen: U = (-Д) +II amRhvorfra I am II am = (U +E) / R

For at begrænse strømmen er en betydelig modstand, normalt lig med to gange startmodstanden, inkluderet i motorens ankerkredsløb. Det særlige ved oppositionstilstanden er, at den mekaniske kraft fra akselsiden og den elektriske energi fra netværket leveres til motoren, og alt dette bruges på at opvarme ankeret: Pm+Re = EI + UI = Аз2(Ри + AZext)

Den modsatte tilstand kan også opnås ved at skifte viklingerne i den modsatte rotationsretning, mens ankeret fortsætter med at rotere i samme retning på grund af reserven af ​​kinetisk energi (for eksempel når maskinen med et reaktivt statisk moment - ventilatoren stopper).

I overensstemmelse med den accepterede betingelse for at læse tegn n og M i henhold til motortilstanden, når motoren skiftes til omvendt rotation, skal de positive retninger af koordinatakserne ændres, det vil sige, at motortilstanden nu vil være i tredje kvadrant, og oppositionen - i den anden.

Således, hvis motoren kørte i motortilstand ved punkt A, vil den på tidspunktet for omskiftning, når hastigheden endnu ikke er ændret, være med en ny karakteristik i anden kvadrant ved punkt D. Stop vil ske nede i karakteristik DE (-n0), og hvis motoren ikke slukkes ved omdrejningstal t = 0, vil den arbejde på denne karakteristik ved punkt E, og rotere maskinen (blæseren) i den modsatte retning ved omdrejningstal -n4.

Elektrodynamisk bremsetilstand

Elektrodynamisk bremsning opnås ved at afbryde motorarmaturet fra netværket og forbinde det til en separat ekstern modstand (fig. 1, anden kvadrant). Denne tilstand adskiller sig naturligvis lidt fra driften af ​​en uafhængigt exciteret DC-generator. Arbejde på en naturlig karakteristik (direkte n0) svarer til kortslutningstilstanden, på grund af høje strømme er bremsning i dette tilfælde kun mulig ved lave hastigheder.

I den elektrodynamiske bremsetilstand er armaturet afbrudt fra U-netværket, derfor: U = 0; ω0 = U / c = 0

Ligningen for mekaniske egenskaber har formen: ω = (-RM) / c2 eller ω = (-Ri + Rext / 9.55se2) M

De mekaniske egenskaber ved elektrodynamisk bremsning er gennem kilden, hvilket betyder, at når hastigheden falder, falder motorens bremsemoment.

Hældningen af ​​egenskaberne bestemmes på samme måde som i motortilstanden af ​​værdien af ​​modstanden i ankerkredsløbet.Elektrodynamisk bremsning er mere økonomisk end det modsatte, da den energi, der forbruges af motoren fra netværket, kun bruges på excitation.

Størrelsen af ​​ankerstrømmen og derfor bremsemomentet afhænger af omdrejningshastigheden og modstanden af ​​ankerkredsløbet: I = -E/ R = -sω /R

Generatortilstand med energiretur til nettet

Denne tilstand er kun mulig, når virkningsretningen af ​​det statiske drejningsmoment falder sammen med motorens drejningsmoment. Under påvirkning af to momenter - motorens drejningsmoment og arbejdsmaskinens drejningsmoment - rotationshastigheden af ​​drevet og f. etc. c. motoren vil begynde at stige, som et resultat vil motorstrømmen og drejningsmomentet falde: I = (U — E)/R= (U — сω)/R

En yderligere stigning i hastigheden fører først til den ideelle tomgangstilstand, når U = E, I = 0 og n = n0, og derefter når e osv. c. motoren bliver mere end den påførte spænding, motoren vil gå i generatortilstand, det vil sige, at den begynder at give energi til netværket.

De mekaniske egenskaber i denne tilstand er en naturlig forlængelse af motortilstandens karakteristika og findes i anden kvadrant. Omdrejningshastigheden har ikke ændret sig, og den forbliver positiv som før, og momentet har et negativt fortegn. I ligningen for de mekaniske egenskaber for generatorens tilstand med energiretur til netværket vil fortegnet for øjeblikket ændre sig, derfor vil det have formen: ω = ωo + (R / c2) M. eller ω = ωo + (R/9,55°Cd3) M.

I praksis bruges den regenerative bremsetilstand kun ved høje hastigheder i drev med potentielle statiske momenter, for eksempel ved sænkning af en last ved høj hastighed.