AC kondensator

Lad os samle kredsløbet med kondensator, hvor generatoren genererer en sinusformet spænding. Lad os analysere sekventielt, hvad der vil ske i kredsløbet, når vi lukker kontakten. Vi vil overveje det indledende øjeblik, når generatorspændingen er lig med nul.

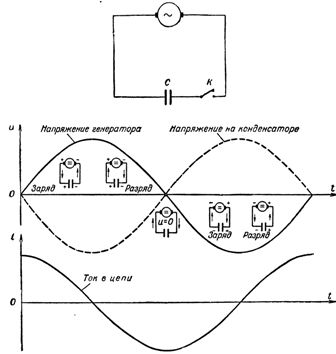
I løbet af det første kvartal af perioden vil spændingen over generatorens terminaler stige, startende fra nul, og kondensatoren begynder at oplade. En strøm vil forekomme i kredsløbet, men i det første øjeblik af opladning af kondensatoren, på trods af at spændingen på dens plader lige er dukket op og stadig er meget lille, vil strømmen i kredsløbet (ladestrømmen) være den største . Når ladningen på kondensatoren stiger, falder strømmen i kredsløbet og når nul i det øjeblik, hvor kondensatoren er fuldt opladet. I dette tilfælde bliver spændingen på kondensatorens plader, strengt efter generatorens spænding, i dette øjeblik maksimal, men med det modsatte fortegn, det vil sige, den er rettet mod generatorens spænding.

Ris. 1. Ændring af strøm og spænding i et kredsløb med kapacitans

På denne måde suser strømmen med den største kraft ind i en kondensator gratis, men begynder straks at falde, når kondensatorens plader er fyldt med ladninger og falder til nul, og oplader den fuldt ud.

Lad os sammenligne dette fænomen med, hvad der sker med strømmen af ​​vand i et rør, der forbinder to kommunikerende beholdere (fig. 2), hvoraf det ene er fyldt og det andet er tomt. Man skal blot trykke på ventilen, der blokerer vandvejen, da vand straks strømmer fra venstre kar under stort tryk gennem røret ind i den tomme højre kar. Umiddelbart vil vandtrykket i røret dog gradvist begynde at svækkes på grund af udligningen af ​​niveauerne i karrene og vil falde til nul. Vandstrømmen vil stoppe.

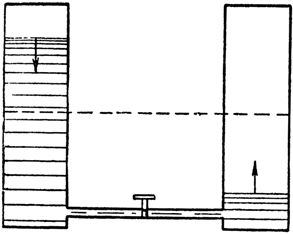
Ris. 2. Ændringen i vandtryk i røret, der forbinder kommunikationsbeholderne, svarer til ændringen i strøm i kredsløbet under opladningen af ​​kondensatoren

På samme måde strømmer strømmen først ind i en uladet kondensator og svækkes derefter gradvist, mens den oplades.

Når den anden fjerdedel af perioden begynder, når generatorspændingen i starten starter langsomt og derefter falder mere og hurtigere, vil den ladede kondensator aflades til generatoren, hvilket forårsager en afladningsstrøm i kredsløbet. Efterhånden som generatorspændingen falder, aflades kondensatoren mere og mere, og afladningsstrømmen i kredsløbet stiger. Retningen af ​​afladningsstrømmen i denne fjerdedel af perioden er modsat retningen af ​​ladestrømmen i periodens første kvartal. Derfor er den aktuelle kurve, der har passeret nulværdien, nu placeret under tidsaksen.

Ved afslutningen af ​​den første halvcyklus nærmer generatorspændingen såvel som kondensatorspændingen sig hurtigt nul, og kredsløbsstrømmen når langsomt sin maksimale værdi. I betragtning af at værdien af ​​strømmen i kredsløbet er større, jo større værdien af ​​ladningen i kredsløbet er, vil det blive klart, hvorfor strømmen når sit maksimum, når spændingen på kondensatorens plader, og derfor ladningen på kondensator, falder hurtigt.

Med begyndelsen af ​​tredje kvartal af perioden begynder kondensatoren at oplade igen, men polariteten af ​​dens plader, såvel som generatorens polaritet, ændres "og omvendt, og strømmen fortsætter med at flyde i det samme retning, begynder at falde, efterhånden som kondensatoren oplades. slutningen af ​​tredje kvartal af perioden, når generator- og kondensatorspændingerne når deres maksimum, går strømmen til nul.

I løbet af den sidste fjerdedel af perioden falder spændingen, faldende, til nul, og strømmen, der har ændret sin retning i kredsløbet, når sin maksimale værdi. Her slutter perioden, hvorefter den næste begynder, præcis gentagelse af den forrige, og så videre.

Under påvirkning af generatorens vekselspænding oplades kondensatoren således to gange i løbet af perioden (det første og tredje kvartal af perioden) og aflades to gange (det andet og fjerde kvartal af perioden). Men da de veksler én efter én kondensator op- og afladninger ledsaget hver gang af passagen af ​​opladnings- og afladningsstrømmen gennem kredsløbet, så kan vi konkludere, at vekselstrøm.

Du kan tjekke dette i følgende simple eksperiment. Tilslut en 4-6 mikrofarad kondensator til lysnettet via en 25 W pære.Lyset tændes og slukker ikke, før kredsløbet er brudt. Dette tyder på, at der er gået en vekselstrøm gennem kredsløbet med kapacitansen. Selvfølgelig passerer den ikke gennem kondensatorens dielektrikum, men repræsenterer på ethvert tidspunkt enten en ladestrøm eller en kondensatorafladningsstrøm.

Som vi ved, er dielektrikumet polariseret under påvirkning af et elektrisk felt, der opstår i det, når kondensatoren oplades, og dets polarisering forsvinder, når kondensatoren aflades.

I dette tilfælde tjener dielektrikumet med forskydningsstrømmen, der opstår i det, til vekselstrømmen som en slags fortsættelse af kredsløbet, og for konstanten bryder det kredsløbet. Men forskydningsstrømmen dannes kun inden for kondensatorens dielektrikum, og derfor forekommer overførslen af ​​ladninger langs kredsløbet ikke.

Modstanden fra en AC-kondensator afhænger af værdien af ​​kondensatorens kapacitans og frekvensen af ​​strømmen.

Jo større kapaciteten af ​​kondensatoren er, jo større er ladningen på kredsløbet under opladning og afladning af kondensatoren og følgelig jo større er strømmen i kredsløbet. En stigning i strømmen i kredsløbet indikerer, at dens modstand er faldet.

Derfor, når kapacitansen stiger, falder kredsløbets modstand mod vekselstrøm.

Det vokser aktuelle frekvens øger mængden af ​​ladning, der føres i kredsløbet, fordi ladningen (såvel som afladningen) af kondensatoren skal ske hurtigere end ved lav frekvens. Samtidig svarer en stigning i mængden af ​​overført ladning pr. tidsenhed til en stigning i strømmen i kredsløbet og derfor til et fald i dets modstand.

Hvis vi på en eller anden måde gradvist reducerer frekvensen af ​​vekselstrømmen og reducerer strømmen til jævnstrøm, så vil modstanden af ​​kondensatoren, der indgår i kredsløbet, gradvist stige og blive uendelig stor (bryder kredsløbet), indtil den vises i konstant strømkredsløb.

Derfor, når frekvensen stiger, falder kondensatorens modstand mod vekselstrøm.

Ligesom modstanden af ​​en spole til en vekselstrøm kaldes induktiv, kaldes modstanden af ​​en kondensator kapacitiv.

Derfor er den kapacitive modstand større, jo lavere kapaciteten af ​​kredsløbet er og frekvensen af ​​strømmen, der føder den.

Kapacitiv modstand er angivet som Xc og måles i ohm.

Den kapacitive modstands afhængighed af strømmens frekvens og kredsløbets kapacitet bestemmes af formlen Xc = 1 /ωC, hvor ω er en cirkulær frekvens lig med produktet af 2πe, C er kredsløbets kapacitet i farads.

Kapacitiv modstand har ligesom induktiv modstand en reaktiv karakter, da kondensatoren ikke forbruger strømkildens energi.

formel Ohms lov for et kapacitivt kredsløb har det formen I = U / Xc, hvor I og U - effektive værdier af strøm og spænding; Xc er kredsløbets kapacitive modstand.

Kondensatorers egenskab til at give høj modstand mod lavfrekvente strømme og let at passere højfrekvente strømme er meget udbredt i kommunikationsudstyrskredsløb.

Ved hjælp af kondensatorer opnås for eksempel adskillelse af konstante strømme og lavfrekvente strømme fra højfrekvente strømme, der er nødvendige for driften af ​​kredsløbene.

Hvis det er nødvendigt at blokere banen for lavfrekvent strøm i den højfrekvente del af kredsløbet, er en lille kondensator forbundet i serie. Den giver stor modstand mod lavfrekvent strøm og passerer samtidig let højfrekvent strøm.

Hvis det er nødvendigt at forhindre højfrekvent strøm, for eksempel i radiostationens strømkredsløb, bruges en kondensator med stor kapacitet, der er forbundet parallelt med strømkilden. I dette tilfælde passerer den højfrekvente strøm gennem kondensatoren og omgår radiostationens strømforsyningskredsløb.

Aktiv modstand og kondensator i AC-kredsløbet

I praksis observeres tilfælde ofte, når de er i et seriekredsløb med en kapacitans aktiv modstand er inkluderet. Kredsløbets samlede modstand i dette tilfælde bestemmes af formlen

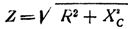
Derfor er den samlede modstand af et kredsløb bestående af aktiv og kapacitiv AC-modstand lig med kvadratroden af ​​summen af ​​kvadraterne af den aktive og kapacitive modstand af dette kredsløb.

Ohms lov forbliver også gyldig for dette I = U / Z kredsløb.

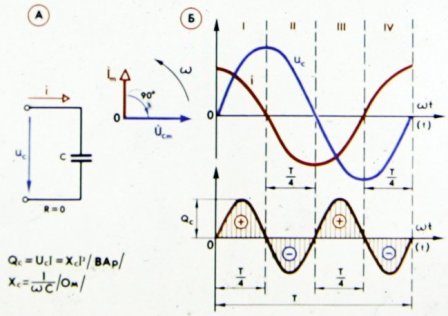
I fig. 3 viser kurverne, der karakteriserer faseforholdet mellem strøm og spænding i et kredsløb indeholdende kapacitiv og aktiv modstand.

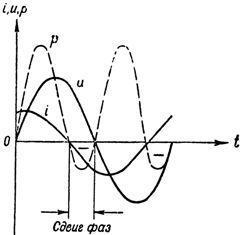
Ris. 3. Strøm, spænding og effekt i et kredsløb med en kondensator og en aktiv modstand

Som det kan ses af figuren, øger strømmen i dette tilfælde spændingen ikke med en fjerdedel af en periode, men med mindre, da den aktive modstand krænker kredsløbets rent kapacitive (reaktive) karakter, som det fremgår af den reducerede fase flytte. Nu er spændingen ved kredsløbsterminalerne defineret som summen af ​​to komponenter: den reaktive komponent af spændingen tive, vil overvinde den kapacitive modstand af kredsløbet og den aktive komponent af spændingen, overvinde dens aktive modstand.

Jo større kredsløbets aktive modstand er, jo mindre faseforskydning mellem strøm og spænding.

Kurven af ​​effektændringen i kredsløbet (se fig. 3) fik to gange i løbet af perioden et negativt fortegn, hvilket, som vi allerede ved, er en konsekvens af kredsløbets reaktive karakter. Jo mindre reaktivt kredsløbet er, jo mindre er faseforskydningen mellem strøm og spænding, og jo mere strømforbruger kredsløbet.

Læs også: Spændingsresonans