Enfaset vekselstrøm

Optagelse af vekselstrøm

Hvis ledningen A drejes i den magnetiske flux, der dannes af magnetens to poler i retning med uret (fig. 1), så vil den, når ledningen krydser magnetfeltlinjerne, fremkalde f.eks. s, hvis værdi bestemmes af udtrykket

E = Blvsinα,

hvor B er den magnetiske induktion i T, l er længden af ​​ledningen i m, v er ledningens hastighed i m/s, α — den vinkel, hvormed ledningen krydser de magnetiske feltlinjer.

Lad B, I og v for dette tilfælde forblive konstante, så den inducerede e. etc. c. vil kun afhænge af vinklen α, hvorved ledningen krydser magnetfeltet. Så ved punkt 1, når ledningen bevæger sig langs magnetfeltlinjerne, er værdien af ​​den inducerede emk. etc. p vil være nul, når ledningen bevæger sig til punkt 3 oe. etc. v. vil være af den største Betydning, da Kraftlinierne vil blive krydset af Lederen i Retningen vinkelret paa dem, og endelig f. Ex. etc. v. vil igen nå nul, hvis ledningen flyttes til punkt 5.

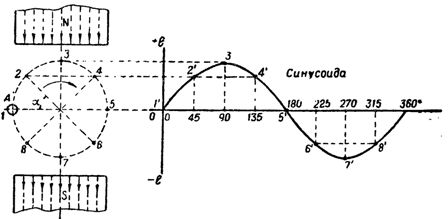
Ris. 1. Ændring af den inducerede e. etc. s. i en ledning, der roterer i et magnetfelt

Ved mellempunkterne 2 og 4, hvor tråden krydser kraftlinjerne i en vinkel α = 45 °, er værdien af ​​den inducerede emk. etc. c. vil være tilsvarende mindre end ved punkt 3. Når ledningen således drejes fra punkt 1 til punkt 5, dvs. med 180°, vil den inducerede e. etc. v. skifter fra nul til maksimum og tilbage til nul.

Det er helt indlysende, at ved en yderligere rotation af tråd A gennem en vinkel på 180° (gennem punkterne 6, 7, 8 og 1), arten af ​​ændringen i den inducerede e. etc. p. vil være den samme, men dens retning vil ændre sig til den modsatte, da tråden vil krydse de magnetiske feltlinjer allerede under den anden pol, hvilket svarer til at krydse dem i den modsatte første retning.

Derfor, når ledningen drejes 360°, vil den inducerede e. etc. v. ændrer sig ikke kun i størrelse hele tiden, men ændrer også retning to gange.

Hvis ledningen er lukket for en vis modstand, vises ledningen elektricitet, også varierende i størrelse og retning.

Elektrisk strøm, der konstant ændrer sig i størrelse og retning, kaldes vekselstrøm.

Hvad er en sinusbølge?

Ændringens art e. etc. (strøm) for en omdrejning af ledningen for større klarhed, er de grafisk repræsenteret ved hjælp af en kurve. Da værdien af ​​e. etc. c. proportionalt med sinα, så er det, efter at have indstillet visse vinkler, muligt ved hjælp af tabeller at bestemme værdien af ​​sinus for hver vinkel, og på den passende skala at konstruere en kurve for ændringen af ​​e. etc. c. For at gøre dette vil vi på den vandrette akse afsætte ledningens rotationsvinkler, og på den lodrette akse, i den passende skala, det inducerede e. etc. med

Hvis tidligere angivet i fig.1 forbinde punkterne med en glat buet linje, så vil det give en idé om størrelsen og arten af ​​ændringen i det inducerede e. etc. (strøm) ved enhver position af lederen i et magnetfelt. På grund af det faktum, at værdien af ​​den inducerede e. etc. p. på ethvert tidspunkt bestemmes af sinus af den vinkel, hvorved tråden krydser magnetfeltet vist i fig. 1 kurve kaldes en sinusformet, og f.eks. etc. s. — sinusformet.

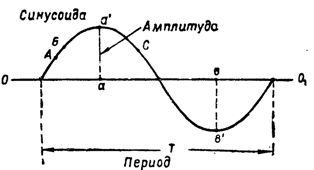
Ris. 2. Sinusoiden og dens karakteristiske værdier

Ændringerne vi så på f.eks. etc. c. svarer sinusformet til ledningens rotation i et magnetfelt i en vinkel på 360°. Når ledningen drejes de næste 360 ​​°, ændres ændringerne i den inducerede e. etc. s.(og strøm) vises igen i en sinusbølge, det vil sige, at de gentages periodisk.

Følgelig forårsaget af denne e. etc. c. kaldes elektrisk strøm sinusformet vekselstrøm... Det er helt indlysende, at den spænding, der kan måles af os ved enderne af ledning A, i nærværelse af et lukket eksternt kredsløb, også vil ændre sig på sinusformet måde.

Vekselstrøm opnået ved at rotere en ledning i en magnetisk flux eller et system af ledninger forbundet i en spole kaldes enfaset vekselstrøm.

Sinusformede vekselstrømme er de mest udbredte inden for teknologi. Du kan dog finde vekselstrømme, der ikke ændrer sig efter sinusloven. Sådanne vekselstrømme kaldes ikke-sinusformet.

Se også: Hvad er vekselstrøm og hvordan adskiller den sig fra jævnstrøm

Amplitude, periode, frekvens af enfaset vekselstrøm

Nuværende styrke, der skifter langs en sinusoide, ændres kontinuerligt. Så hvis strømmen i punkt A (fig. 2) er lig med 3a, så vil den i punkt B allerede være større.På et andet punkt på sinusoiden, for eksempel ved punkt C, vil strømmen nu have en ny værdi, og så videre.

Strømstyrken på bestemte tidspunkter, når den ændrer sig langs en sinusformet, kaldes øjeblikkelige strømværdier.

Den største øjeblikkelige værdi af en enfaset vekselstrøm kaldes, når den ændrer sig langs en sinusformet amplitude... Det er let at se, at for en omdrejning af ledningen når strømmen sin amplitudeværdi to gange. En af værdierne af aa 'er positiv og er tegnet op fra 001-aksen og den anden bv' er negativ og trækkes ned fra aksen.

Den tid, hvor den inducerede e. etc. (eller den aktuelle kraft) gennemgår hele forandringscyklussen, den såkaldte månedlige cyklus T (fig. 2). Perioden måles normalt i sekunder.

Periodens gensidige kaldes frekvensen (f). Med andre ord, vekselstrømsfrekvens er antallet af perioder per tidsenhed, dvs. på sekunder. Så for eksempel, hvis en vekselstrøm inden for 1 sekund antager de samme værdier og retning ti gange, så vil frekvensen af ​​en sådan vekselstrøm være 10 perioder i sekundet.

For at måle frekvensen bruges i stedet for antallet af perioder i sekundet en enhed kaldet hertz (hertz). En frekvens på 1 hertz er lig med en frekvens på 1 lps/sek. Ved måling af høje frekvenser er det mere bekvemt at bruge en enhed 1000 gange større end hertz, dvs. kilohertz (kHz), eller 1.000.000 gange større end hertz - megahertz (mhz).

Vekselstrømme, der anvendes i teknologien, kan afhængigt af frekvensen opdeles i lavfrekvente strømme og højfrekvente strømme.

AC rms værdi

Jævnstrøm, der passerer gennem ledningen, opvarmer den. Hvis du kører vekselstrøm gennem ledningen, bliver ledningen også varmet op.Det er forståeligt, for selvom vekselstrømmen hele tiden ændrer retning, afhænger afgivelsen af ​​varme slet ikke af strømmens retning i ledningen.

Når vekselstrøm føres gennem en pære, vil dens glødetråd lyse. Ved en standard vekselstrømsfrekvens på 50 Hz vil der ikke være nogen flimren af ​​lyset, fordi glødepærens glødetråd, der har termisk inerti, ikke har tid til at køle ned på de tidspunkter, hvor strømmen i kredsløbet er nul. Brugen af ​​vekselstrøm med en frekvens på mindre end 50 Hz til belysning er nu uønsket på grund af det faktum, at der opstår ubehagelige, øjentrættende udsving i pærens intensitet.

Hvis vi fortsætter jævnstrømsanalogien, kan vi forvente, at en vekselstrøm, der løber gennem en ledning, skaber omkring den magnetfelt. Faktisk nVekselstrøm skaber ikke et magnetfelt, men fordi det magnetiske felt, det skaber, også vil være variabelt i retning og størrelse.

En vekselstrøm ændrer sig hele tiden i både størrelse og retningNS. Naturligvis opstår spørgsmålet om, hvordan man måler variablen T brønd, og hvad dens værdi, når man skifter langs en sinusoide, skal betragtes som årsag til denne eller hin handling.

C Til dette formål sammenlignes vekselstrøm med hensyn til den virkning, den frembringer med jævnstrøm, hvis værdi forbliver uændret under forsøget.

Antag, at der løber en jævnstrøm gennem en ledning med konstant modstand 10 A, og det viser sig, at ledningen opvarmes til en temperatur på 50 °.Hvis vi nu passerer gennem den samme ledning ikke en jævnstrøm, men en vekselstrøm, og så vælger vi dens værdi (virker f.eks. med en rheostat), så ledningen også opvarmes til en temperatur på 50°, så i i dette tilfælde kan vi sige, at virkningen af ​​vekselstrøm er lig med virkningen af ​​jævnstrøm.

Opvarmning af ledningen i begge tilfælde til samme temperatur viser, at i en tidsenhed afgiver vekselstrømmen i ledningen samme mængde varme som jævnstrømmen.

En sinusformet vekselstrøm, der for en given modstand pr. tidsenhed udsender den samme mængde varme som en jævnstrøm, der i størrelsesorden svarer til en jævnstrøm... Denne strømværdi kaldes den effektive (Id) eller effektive værdi af vekselstrøm .. Derfor, for vores eksempel, vil den effektive værdi af vekselstrøm være 10 A... I dette tilfælde vil de maksimale (spids-) strømværdier overstige gennemsnitsværdierne i størrelsesorden.

Erfaringer og beregninger viser, at de effektive værdier af vekselstrøm er mindre end dens amplitudeværdier i √2 (1,41) gange. Derfor, hvis spidsværdien af ​​strømmen er kendt, så kan den effektive værdi af strømmen Id bestemmes ved at dividere amplituden af ​​strømmen Ia med √2, dvs. Id = Aza/√2

Omvendt, hvis rms værdien af ​​strømmen er kendt, så kan spidsværdien af ​​strømmen beregnes, dvs. Ia = Azd√2

De samme relationer vil gælde for amplituden og rms-værdierne for f. etc. v. og spændinger: Enhed = Ea /√2, Ud = Uа/√2

Måleapparater viser oftest de faktiske værdier, derfor udelades indekset «d» normalt ved notation, men du bør ikke glemme det.

Impedans i AC-kredsløb

Når induktans- og kapacitansforbrugere er tilsluttet AC-kredsløbet, skal både aktiv og reaktans tages i betragtning (reaktans opstår, når en kondensator er tændt eller drosler i et AC-kredsløb). Derfor, når man bestemmer strømmen, der passerer gennem en sådan forbruger, er det nødvendigt at dividere forsyningsspændingen med impedansen af ​​kredsløbet (forbrugeren).

Impedansen (Z) af et enkeltfaset AC-kredsløb bestemmes af følgende formel:

Z = √(R2 + (ωL — 1 / ωC)2

hvor R er kredsløbets aktive modstand i ohm, L er kredsløbets induktans i henries, C er kredsløbets (kondensator) kapacitans i farad, ω — vekselstrøms vinkelfrekvens.

Forskellige forbrugere bruges i vekselstrømkredsløb, hvor det er nødvendigt at overveje enten de tre værdier af R, L, C eller kun nogle af dem. Samtidig skal der tages hensyn til vekselstrømmens vinkelfrekvens.

For nogle brugere kan kun værdierne af R og L tages i betragtning ved de tilsvarende hjørnefrekvensværdier. For eksempel ved en AC-frekvens på 50 Hz magnetspole eller generatorviklingen kan kun anses for at indeholde aktiv og induktiv modstand. Med andre ord kan kapacitansen i dette tilfælde negligeres. Så kan AC-impedansen for en sådan bruger beregnes med formlen:

Z = √(R2 + ω2L2)

Hvis en sådan spole eller en spole designet til vekselstrømsdrift er forbundet med en jævnstrøm af samme spænding, vil der gå en meget stor strøm gennem spolen, hvilket kan føre til betydelig varmeudvikling, og spolens isolering kan blive beskadiget Tværtimod vil en lille strøm strømme gennem en spole designet til at fungere i et jævnstrømskredsløb og forbundet til et vekselstrømkredsløb med samme spænding, og enheden, hvori denne spole bruges, vil ikke udføre den nødvendige handling.

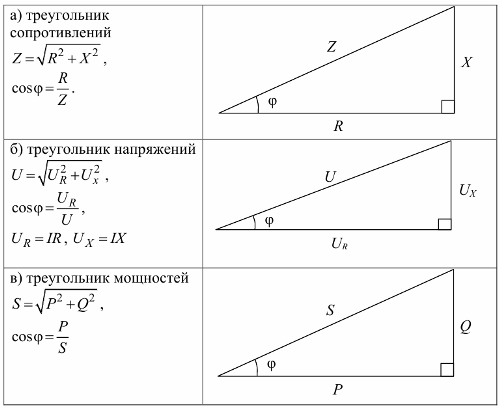
Modstandstrekant, spændingstrekant og effekttrekant: