Bølgeform og spændingsmåling

Formen på spændings- og strømkurverne anses for at være praktisk sinusformet, hvis nogen af ​​dens ordinater afviger fra den tilsvarende ordinat af en sinusformet lig med den i amplitude, med et segment, der ikke overstiger 5 % af amplituden.

Sinusoidalitet kan testes på flere måder. Brug den enkleste af dem til at observere den undersøgte kurve på skærmen af ​​et katodestråleoscilloskop.

Til dette er to identiske sinusformede linjer tidligere tegnet på enhedens skærm eller på en gennemsigtig plade, forskudt lodret i forhold til hinanden med 10% af deres amplitude (fig. 1).

Spændingen, der testes, påføres derefter oscilloskopets Y-indgang, og ved at justere forstærkningen på Y-kanalen og sweep-perioden dimensioneres skærmkurven, så den ligger inden for det bånd, der er begrænset af hjælpesinusoiderne. Hvis dette lykkes, anses spændingen for at være praktisk talt sinusformet.

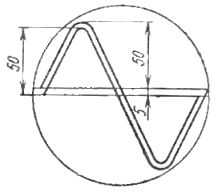
Ris. 1. Hjælpekurver til bestemmelse af strøm- og spændingsform ved hjælp af et katodestråleoscilloskop

For at overveje den anden måde at bestemme sinusoidaliteten af ​​en kurve på, introducerer vi flere definitioner. Som du ved, kan værdien af ​​en periodisk variabel karakteriseres ved de effektive, gennemsnitlige og maksimale (amplitude) værdier. Hvis den periodiske mængde x ændres i henhold til en sinusformet lov, er alle dens værdier relateret til hinanden på en bestemt måde.

For eksempel forholdet mellem amplitudeværdien og den effektive værdi, kaldet topkoefficienten ka = xm/ x = √2 = 1,41, forholdet mellem gennemsnitsværdien i en halv periode og amplitudeværdien, kaldet gennemsnitsværdikoefficienten kCp = xcp / xm = 2 /π = 0,637 og til sidst forholdet mellem den effektive værdi og gennemsnitsværdien, kaldet billedformatet ke = x / xCp = π / (2√2) = 1,11.

Med fokus på disse forhold giver standarden mulighed for at bestemme den sinusformede form af kurven for en periodisk mængde baseret på resultaterne af den samtidige måling af de gennemsnitlige og effektive værdier. Kurven anses for næsten sinusformet, hvis 1,132> km/t> 1,088.

På grund af det faktum, at de fleste af de måleinstrumenter, der anvendes i praksis, er kalibreret i gennemsnitsværdier, er det ikke altid muligt direkte at måle middel- og medianværdier. I dette tilfælde måles den undersøgte værdi samtidigt med amplitude (peak) og elektrodynamiske voltmetre. Hvis det er nødvendigt at bestemme alle tre navngivne koefficienter, skal der tilsluttes et ensrettervoltmeter.

Aflæsningerne af voltmeteret og koefficienterne, der karakteriserer formens sinusoidalitet, er relateret til følgende forhold: ka = 1,41U1/ U2, кf = U2/0,9U3, kcp = 0,673 = U3/ U1, hvor U1, U2, U3 — aflæsninger af amplitude-, elektrodynamiske og ensretterskalavoltmetre kalibreret i sinusformede middelspændingsværdier.

Et eksempel. For at bestemme den ikke-sinusformede form af spændingskurven af ​​transformatorens sekundære vikling måles fasespændingen samtidigt med amplitude V3-43, elektrodynamisk D-556 og ensretter Ts4317 voltmetre.

Deres aflæsninger var U1 = 76 V, U2 = 61 V, U3 = 59,5 V. Derefter ka = 1,41 x 76/61 = 1,76, ke = 1,11 x 61 / 59,5 = 1, 14, kcp = 0,637 x 569,5 / .

På grund af det faktum, at disse koefficienter for en sinusformet kurve skal være henholdsvis 1,41, 1,11 og 0,637, kan det konkluderes, at spændingen af ​​transformatorens sekundære vikling har en ikke-sinusformet form. Vær opmærksom på, at med en sinusformet spænding skal aflæsningerne af alle tre voltmetre være ens.