Kontinuerlige svingninger og parametrisk resonans

Kontinuerlige vibrationer — vibrationer, hvis energi ikke ændrer sig over tid. I virkelige fysiske systemer er der altid årsager, der forårsager overgangen af ​​vibrationsenergi til termisk energi (f.eks. friktion i mekaniske systemer, aktiv modstand i elektriske systemer).

Derfor kan udæmpede svingninger kun opnås, forudsat at disse energitab genopbygges. En sådan genopfyldning sker automatisk i selvoscillerende systemer på grund af energi fra en ekstern kilde. Kontinuerlige elektromagnetiske svingninger er ekstremt udbredt. Forskellige generatorer bruges til at få dem.

For at gøre elektriske eller mekaniske vibrationer (af en oscillerende cirkel eller pendul) udæmpede, er det nødvendigt at kompensere for modstands- eller friktionstab til enhver tid.

For eksempel kan du handle på det oscillerende kredsløb med en vekslende EMF, som periodisk vil øge strømmen i spolen og følgelig opretholde spændingsamplituden i kondensatoren.Eller du kan skubbe pendulet på lignende måde og holde det svingende harmonisk.

Som du ved, er størrelsen af ​​energien i magnetfeltet i spolen i det oscillerende kredsløb relateret til dets induktans og strøm ved følgende forhold (den anden formel erenergi af kondensatorens elektriske felt samme kontur kontur)

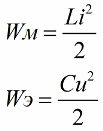
Det er klart fra den første formel, at hvis vi med jævne mellemrum øger strømmen i spolen, der virker på det vekslende EMF-kredsløb, så (ved at øge eller formindske den anden faktor i formlen - strømmen) vil vi periodisk genopfylde dette kredsløb med energi.

Virker på kredsløbet strengt i tide med dets naturlige frie svingninger, det vil sige ved resonansfrekvensen, vil vi få fænomenet elektrisk resonans, fordi det er på resonansfrekvensen oscillerende system absorberer den energi, der tilføres den mest intensivt.

Men hvad hvis du med jævne mellemrum ikke ændrer den anden faktor (ikke strøm eller spænding), men den første faktor - induktans eller kapacitans? I dette tilfælde vil kredsløbet også gennemgå en ændring i sin energi.

For eksempel periodisk at skubbe kernen ind og ud af spolen eller skubbe ind og ud af kondensatorendielektrisk, — vi får også en meget bestemt periodisk ændring af energien i kredsløbet.

Vi skriver denne position for en enhedsændring i spoleinduktans:

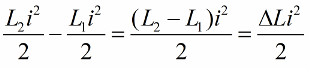
Den mest udtalte effekt af kredsløbssvinget vil være, hvis induktansændringerne foretages lige i tide. For eksempel, hvis vi tager det samme kredsløb på et hvilket som helst tidspunkt, når en strøm i allerede flyder gennem det, og indfører en kerne i spolen, så vil energien ændre sig med følgende mængde:

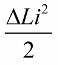
Lad nu frie svingninger opstå i selve kredsløbet, men i det øjeblik, hvor energien efter en kvart periode er gået helt ind i kondensatoren og strømmen i spolen er blevet nul, vil vi brat fjerne kernen fra spolen Induktansen vil vende tilbage til sin oprindelige tilstand, til startværdien L. Der skal ikke bruges arbejde mod magnetfeltet, når kernen fjernes. Derfor, da kernen blev skubbet ind i spolen, modtog kredsløbet energi, da vi arbejdede, hvis værdi:

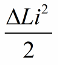
Efter en fjerdedel af perioden begynder kondensatoren at aflade, dens energi omdannes igen til energien fra spolens magnetfelt Når magnetfeltet når amplitude, vil vi igen trykke skarpt på kernen. Igen steg induktansen, steget med samme mængde.

Og igen, ved nul strøm, returnerer vi induktansen til dens oprindelige værdi. Som et resultat heraf, hvis energiforstærkningerne for hver halvcyklus overstiger modstandstabene, vil løkkens energi stige hele tiden, og oscillationsamplituden vil stige. Denne situation kommer til udtryk ved uligheden:

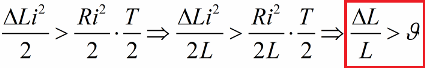
Her dividerede vi begge sider af denne ulighed med L og nedskrev betingelsen for muligheden for parametrisk excitation ved spring for en vis værdi af den logaritmiske dekrement.

Det anbefales at ændre induktansen (eller kapacitansen) to gange pr. periode, derfor bør frekvensen af ​​parameterændringen (parametrisk resonansfrekvens) være to gange den naturlige frekvens af det oscillerende system:

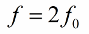
Så banen til excitation af oscillationer i kredsløbet er dukket op uden behov for direkte at ændre EMF eller strøm.Den indledende fluktuerende strøm i kredsløbet er altid til stede på den ene eller anden måde, og det tager ikke engang hensyn til interferens fra radiofrekvenssvingninger i atmosfæren.

Hvis induktansen (eller kapacitansen) ikke ændres i hop, men harmonisk, vil betingelsen for forekomsten af ​​svingninger se lidt anderledes ud:

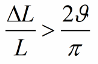
Da kapacitans og induktans er kredsløbsparametre (såsom massen af ​​et pendul eller elasticiteten af ​​en fjeder), kaldes metoden til excitation af oscillationer også for parametrisk excitation.

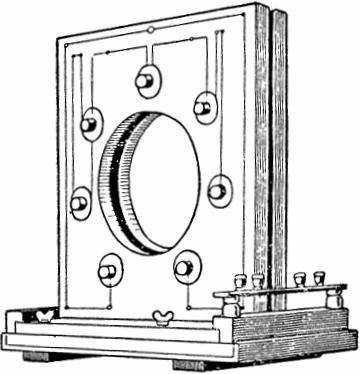
Dette fænomen blev opdaget og praktisk undersøgt i begyndelsen af ​​det 20. århundrede af de sovjetiske fysikere Mandelstam og Papalexi. Baseret på dette fysiske fænomen byggede de den første parametriske AC-generator med en effekt på 4 kW og variabel induktans.

I udformningen af ​​generatoren var syv par flade spoler placeret på begge sider af rammen, i hvis hulrum en ferromagnetisk skive med fremspring roterede. Når skiven drives til at rotere af en motor, bevæger dens fremspring periodisk sig ind og ud af rummet mellem hvert par spoler, hvorved induktansen ændres og oscillationerne stimuleres.