Oscillerende proces i elektroteknik og elektronik, typer af svingninger
Oscillerende proces - en proces med varierende grader af repeterbarhed. Alle oscillerende processer er opdelt i 2 klasser: periodiske og ikke-periodiske. I teorien bruger de også en mellemklasse - næsten periodiske svingninger.
En oscillerende proces kaldes periodisk, hvor værdien, der kendetegner denne proces, taget til enhver tid efter en vis tidsperiode T har samme værdi.
Funktionen f (t), som er et matematisk udtryk for den svingende proces, kaldes periodisk med periode T, hvis den opfylder betingelsen f (t + T) = f (t).
Blandt klassen af periodiske oscillerende processer spilles hovedrollen af harmoniske eller sinusformede svingninger, hvor en ændring i en fysisk mængde med tiden sker i henhold til loven om sinus eller cosinus. Deres samlede rekord er:
y = f (t) = aCos ((2π / T) t — φ),
hvor a — amplitude af svingninger, φ er oscillationsfasen, 1 /T = f — frekvens og 2πf = ω — frekvens af cykliske eller cirkulære vibrationer.
Anvendelse af sinusformede svingninger og deres egenskaber:
Grundlæggende parametre for AC
Grafiske måder at vise vekselstrøm på
En næsten periodisk funktion svarende til en aflæsning af periodiske svingninger er defineret af betingelsen:
| f · (t + τ) — f (t) | <= ε hvor ε — tildel en værdi til hver værdi T.
Mængden τ i dette tilfælde kaldes næsten punktum. Hvis værdien ε er meget lille sammenlignet med gennemsnitsværdien af f (t) på tidspunktet T, så vil den kvasi-periodiske funktion være tæt på den periodiske.
Ikke-periodiske svingninger er meget mere varierede end periodiske. Men oftest i automation skal man møde dæmpning eller stigende sinusformede svingninger.
Oscillationer i henhold til loven om den dæmpede sinusoide eller, som de nogle gange kaldes, dæmpede harmoniske svingninger, kan repræsenteres i en generel form:
x = Ae-δTcos·(ω + φ),
hvor t er tid, A og φ er vilkårlige konstanter. Den generelle notation af loven om stigende harmoniske svingninger adskiller sig kun i tegnet på dæmpningsfaktoren δ[1 sekund].
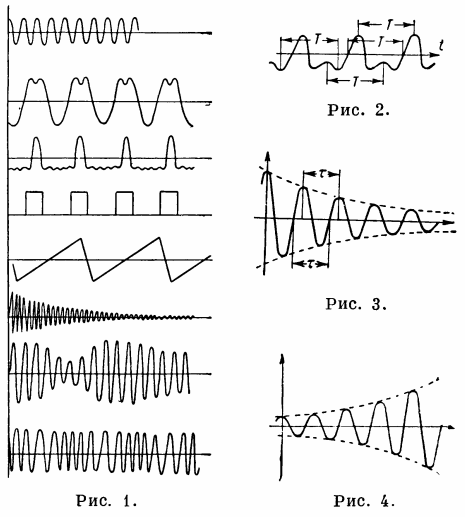
Fig. 1 — oscillerende proces, Fig. 2. — periodisk proces, fig. 3. — henfaldende harmoniske svingninger, fig. 4. — stigning i harmoniske svingninger.
Et eksempel på anvendelsen af den oscillerende proces er det enkleste oscillerende kredsløb.
Oscillatorkredsløb (elektrisk kredsløb) - et passivt elektrisk kredsløb, hvor elektriske svingninger kan forekomme med en frekvens bestemt af parametrene for selve kredsløbet.
Det enkleste oscillerende kredsløb består af kapacitans C og induktans L. I fravær af ekstern påvirkning vil dæmpningssvingninger med frekvensen εО = 1/2π√LC.
Amplituden af vibrationerne falder med fx-δT, hvor δ er dæmpningskoefficienten. Hvis δ> = eO, bliver de dæmpede svingninger i kredsløbet ikke-periodiske.
I elektronik bestemmes kvaliteten af det oscillerende kredsløb af kvalitetsfaktoren: Q = nf/δ... Når en ekstern periodisk kraft virker på det oscillerende kredsløb, opstår der tvangssvingninger i det. Amplituden af tvangssvingninger stiger markant for høj-Q-kredsløb, hvis frekvensen af den ydre påvirkning er tæt på eo (resonans). Oscillerende kredsløb er en af hoveddelene i resonansforstærkere, generatorer og andre elektroniske enheder.
Se også om dette emne: Anvendelse af spændingsresonans og strømresonans
