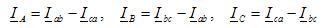Beregning af trefasede kredsløb

Kæde trefaset vekselstrøm består af en trefaset strømforsyning, en trefaset forbruger og kommunikationsledningerne mellem dem.

En symmetrisk trefaset forsyning kan repræsenteres som tre enfasede forsyninger, der arbejder ved samme frekvens med samme spænding og med en fasevinkel i tid på 120°. Disse kilder kan være stjerne- eller deltaforbundne.

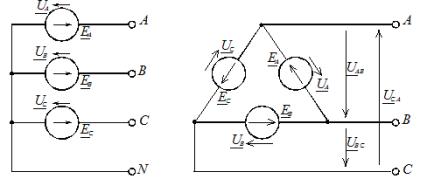
Når den er forbundet i en stjerne, bruges den betingede begyndelse af faserne til at forbinde tre lineære ledere A, B, C, og enderne af faserne er forenet i et punkt, kaldet strømkildens neutrale punkt (trefaset generator eller transformer). Til dette punkt kan tilsluttes en neutral ledning N. Stjerneforbindelsesdiagrammet for strømkilden er vist i figur 1, a.

Ris. 1. Tilslutningsdiagrammer over strømforsyningsfaserne: a — stjerne; b - trekant

Spændingen mellem linje og nulleder kaldes fase og mellem linjeledere kaldes linje (for flere detaljer se her – Linje- og fasespænding).

V integreret form indtastningerne af udtrykkene for fasespændingerne er:

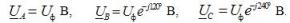
De tilsvarende netspændinger ved stjernetilslutning:

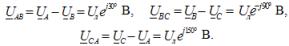
Her er Uf strømkildens fasespændingsmodul, og Ul er linjespændingsmodulet. I et symmetrisk trefasesystem, når kildefaserne er stjerneforbundne, er der en sammenhæng mellem disse spændinger:

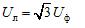
Når faserne er forbundet med en trekant, er fasestrømforsyningerne forbundet i serie i en lukket sløjfe (figur 1, b).

Tre lineære ledninger A, B, C bringes ud fra de punkter, hvor kilderne kombineres med hinanden, og går til belastningen. Af figur 1, b, kan det ses, at fasekildernes udgange er forbundet med lineære ledninger, og derfor, når kildens faser er forbundet med en trekant, er fasespændingerne lig med lineære. I dette tilfælde er der ingen neutral ledning.

En belastning kan tilsluttes en trefaset forsyning. Med hensyn til størrelse og natur kan en trefaset belastning være symmetrisk og asymmetrisk.

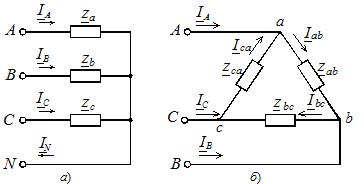
I tilfælde af en symmetrisk belastning er de komplekse modstande af de tre faser de samme, og hvis disse modstande er forskellige, så er belastningen ubalanceret. Belastningsfaserne kan forbindes med hinanden med stjerne eller trekant (figur 2), uanset kildetilslutningsskemaet.

Ris. 2. Indlæs fasetilslutningsdiagrammer

Stjerneforbindelsen kan være med eller uden neutral ledning (se figur 2, a). Fraværet af en neutral ledning eliminerer den stive forbindelse af belastningsspændingen til forsyningsspændingen, og i tilfælde af en asymmetrisk fasebelastning er disse spændinger ikke lig med hinanden.For at skelne dem blev vi enige om at bruge store bogstaver i bogstavbetegnelsesindekserne for forsyningsspændingerne og -strømmene, og små bogstaver i de belastningsspecifikke parametre.

Algoritmen til at analysere et trefaset kredsløb afhænger af belastningsforbindelsesskemaet, de indledende parametre og formålet med beregningen.

To-node-metoden bruges til at bestemme fasespændingerne med en ubalanceret stjerneforbundet belastning uden en nulleder. Ifølge denne metode begynder beregningen med bestemmelsen af ​​spændingen UN mellem forsyningens nulpunkter og belastningen, kaldet den neutrale afvigelsesspænding:

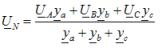
hvor ya, yb, yc - tilladte værdier af de tilsvarende belastningsfaser i kompleks form

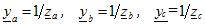
Spændingerne over faserne af en ubalanceret belastning findes ud fra udtrykkene:

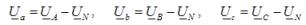
I det specielle tilfælde af belastningsubalance, når der i mangel af en nulleder opstår en kortslutning i en af ​​belastningsfaserne, er den neutrale forspænding lig med fasespændingen af ​​forsyningen til den fase, hvor kortslutningen fandt sted.

Spændingen på belastningens lukkede fase er nul, og på de to andre er den numerisk lig med linjespændingen. Antag for eksempel, at der opstår en kortslutning i fase B. Den neutrale forspænding i dette tilfælde er UN = UB. Så fasespændingerne på belastningen:

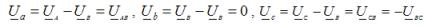
Fasestrømme i belastningen, de er også linjelederstrømme for enhver type belastning:

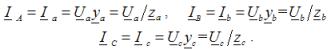
I opgaverne ved beregning af trefasede kredsløb overvejes tre muligheder for at forbinde trefasede forbrugere med en stjerne: forbindelse til en neutral ledning i tilstedeværelse af forbrugere i tre faser, tilslutning til en neutral ledning i fravær af forbrugere i en af faserne, og tilslutning uden neutral ledning med en kort forbindelse i en af ​​belastningsfaserne...

I den første og anden version er de tilsvarende fasespændinger af forsyningen placeret på belastningsfaserne, og fasestrømmene i belastningen bestemmes af ovenstående formler.

I den tredje version er spændingen af ​​belastningsfaserne ikke lig med forsyningens fasespænding og bestemmes ved hjælp af afhængighederne

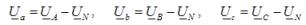
Strømmene i to ukortlagte faser bestemmes i henhold til Ohms lov, som en brøkdel af divisionen af ​​fasespændingen med impedansen af ​​den respektive fase. Kortslutningsstrømmen bestemmes ved hjælp af en ligning baseret på Kirchhoffs første lovkompileret for belastningens neutrale punkt.

For ovenstående eksempel på en fase B kortslutning:

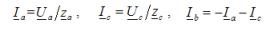
For hver type belastning er den trefasede aktive og reaktive effekt lig med summen af ​​henholdsvis den aktive og reaktive effekt af de enkelte faser. For at bestemme disse fasekræfter kan du bruge udtrykket

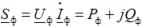
hvor Uf,Azf, er komplekset af spændingen og komplekset af koblede strømme i belastningsfasen; Pf, Qf — aktiv og reaktiv effekt i belastningsfasen.

Trefaset aktiv effekt: P = Pa + Pb + Pc

Trefaset reaktiv effekt: Q = Qa + Qb + Vc

Trefaset tilsyneladende strøm:

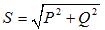
Når forbrugere er forbundet med en trekant, har kredsløbet den form, der er vist i figur 2, b. I denne tilstand er fasetilslutningen af ​​den balancerede strømforsyning irrelevant.

Spændinger mellem strømforsyningsledningerne detekteres på belastningsfaserne. Fasestrømmene i belastningen bestemmes vha Ohms lov for en del af et kredsløbAzf = Uf /zf, hvor Uf — fasespænding i belastningen (svarende til strømkildens netspænding); zf er den samlede modstand af den tilsvarende fase af belastningen.

Strømme i lineære ledere bestemmes af fasestrømme baseret på Kirchhoffs første lov for hver knude (punkt a, b, c) i kredsløbet vist i figur 2, b: