Beregning af potentiometer og sammensat shunt

Begreber og formler

Et potentiometer er en variabel modstand med en skyder, der er inkluderet som vist i fig.

For flere detaljer se - Potentiometre og deres anvendelser

En spænding U påføres punkt 1 og 2. En justerbar spænding fjernes fra punkt 2 og 3, hvis værdi er mindre end U og afhænger af skyderens position. Spændingsdelere har et lignende skema, men de er ikke justerbare og har ikke en bevægelig skyder.

Potentiometre, spændingsdelere og komplekse shunts beregnes vha Kirchhoffs love, såsom beregning af konventionelle kredsløb med modstande.

Eksempler på

1. Kildespændingen er U = 24 V, potentiometerets samlede modstand er r = 300 Ohm. Motoren monteres separat således at r1 = 50 ohm. Hvilken spænding U1 kan fjernes fra punkt 3 og 2 (fig. 1)?

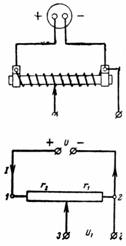
Ris. 1.

Strømmen I og spændingen U over modstanden r er forbundet med formlen I ∙ r = U.

Potentiometerskyderen adskiller noget af modstanden, dvs. modstanden r1. Spændingsfaldet mellem punkt 3 og 2 er lig med I ∙ r1 = U1.

Ud fra forholdet mellem spændingsfaldet får vi ligheden (I ∙ r1) / (I ∙ r) = U1 / U. Jo større modstand r1, jo større er værdien af ​​spændingen U1 mellem punkterne 3 og 2 U1 = r1 / r ∙ U = 50/300 ∙ 24 = 4 V.

2. Potentiometeret (fig. 2) er belastet på en lampe med modstand r = 100 Ohm. Potentiometeret er opdelt med en skyder i to dele med r1 = 600 Ohm og r2 = 200 Ohm. Bestem spændingen Ul og lampestrømmen Il.

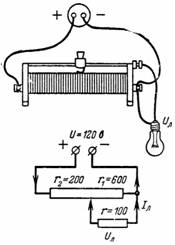
Ris. 2.

Strøm I løber gennem modstand r2 og strøm Il løber gennem lampen. En strøm I-Il løber gennem modstanden r1, som skaber en spænding over modstanden r1, der er lig med lampespændingen: (I-Il) ∙ r1 = Ul.

På den anden side er lampespændingen lig med kildespændingen minus spændingsfald ved modstand r2: U-I ∙ r2 = Ul.

Strømmen I er lig med kildespændingen divideret med den resulterende modstand af den serie-parallelle forbindelse af modstandene:

I = U / (r2 + (r ∙ r1) / (r + r1)).

Vi erstatter udtrykket for den samlede strøm af kilden i den anden ligning:

U-U / (r2 + (r ∙ r1) / (r + r1)) ∙ r2 = Ul.

Efter transformationen får vi et udtryk for lampespændingen:

Ul = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) ∙ r.

Hvis vi transformerer dette udtryk, ud fra det faktum, at Ul = Il ∙ r, får vi et udtryk for lampestrømmen:

Il = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r).

Erstat de numeriske værdier i de resulterende ligninger:

Ul = (120 ∙ 600) / (600 ∙ 200 + 600 ∙ 100 + 200 ∙ 100) ∙ 100 = 7200000/200000 = 36 V;

Il = Ul/r = 36/100 = 0,36 A.

3. Beregn spændingen Up og strømmen Ip for måleapparatet, der er tilsluttet en del af potentiometeret. Enheden har en modstand på r = 1000 Ohm. Forgreningspunktet deler modstanden af ​​deleren i r2 = 500 ohm og r1 = 7000 ohm (fig. 3).Spænding ved terminalerne på potentiometeret U = 220 V.

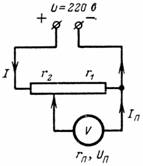
Ris. 3.

Ved at bruge de tidligere opnåede formler kan vi skrive, at strømmen, der strømmer gennem enheden, er:

In = (U ∙ r1) / (r1 ∙ r2 + r1 ∙ r + r2 ∙ r) = (220 ∙ 7000) / (7000 ∙ 500 + 7000 ∙ 1000 + 500 ∙0 = 010 500 = 010 500 = 010 500) 1,54 / 11 = 0,14 A.

Op = Ip ∙ r = 0,14 ∙ 1000 = 14 V.

4. Beregn spændingen af ​​enheden Up, hvis den bruger en strøm Ip = 20 mA og er forbundet til et potentiometer opdelt i modstande r2 = 10 ^ 4 Ohm og r1 = 2 ∙ 10 ^ 4 Ohm (fig. 3).

Den samlede spænding i spændingsdeleren er lig med summen af ​​spændingsfaldene i dens dele (gennem modstandene r1 og r2): U = I ∙ r2 + I1 ∙ r1; U = I ∙ r2 + Op

Kildestrømmen er forgrenet ved motorens kontaktpunkt: I = I1 + Ip; I = Upn / r1 + In.

Vi erstatter værdien af ​​strømmen I i spændingsligningen:

U = (Un / r1 + In) ∙ r2 + Un;

U = Uп / r1 ∙ r2 + Iп ∙ r2 + Uп;

U = Upn ∙ (r2 / r1 +1) + In ∙ r2.

Derfor er enhedsspændingen Upn = (U-In ∙ r2) / (r1 + r2) ∙ r1.

Erstat de numeriske værdier: Op = (220-0,02 ∙ 10000) / 30000 ∙ 20000 = 20/3 ∙ 2 = 13,3 V.

5. En jævnstrømskilde med spænding U = 120 V forsyner radiomodtagerens anodekredsløb gennem et potentiometer (spændingsdeler), som sammen med filteret har en modstand på r = 10000 Ohm. Spændingen U1 fjernes af modstanden r2 = 8000 Ohm. Beregn anodespændingen ved ingen belastning og ved belastningsstrøm I = 0,02 A (fig. 4).

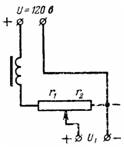
Ris. 4.

Det første tilfælde ligner eksempel 1:

U: U1 = r: r2;

U1 = r2 / r ∙ U = 8000/10000 ∙ 120 = 96 V.

Det andet tilfælde ligner eksempel 3:

U1 = (U-I ∙ r1) / r ∙ r2;

U1 = (120-0,02 ∙ 2000) / 10000 ∙ 8000 = 64 V.

Ved opladning falder spændingen fra 96 ​​til 64 V.Hvis der er behov for mere spænding, skal skyderen flyttes til venstre, det vil sige, at modstanden r2 skal øges.

6. Spændinger Ua og Ub fjernes af spændingsdeleren. Den samlede modstand af spændingsdeleren forbundet med spændingen U1 = 220 V er r = 20.000 Ohm. Hvad er spændingen Ua i modstanden r3 = 12000 Ohm med strømforbrug Ia = 0,01 A og spændingen Ub i modstanden r2 + r3 = 18000 Ohm med strømforbrug Ib = 0,02 A (fig. 5).

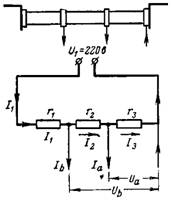
Ris. 5.

Spændingsmodstand r3

Ua = I3 ∙ r3;

Ua = (U -Ia ∙ (r1 + r2) -Ib ∙ r1) / r ∙ r3;

Ua = (220-0,01 ∙ 8000-0,02 ∙ 2000) / 20 000 ∙ 12000 = (220-80-40) / 20 ∙ 12 = 60 V.

Spændingen Ub er lig med summen af ​​spændingsfaldet Ua over modstanden r3 og spændingsfaldet over modstanden r2. Spændingsfaldet over modstand r2 er lig med I2 ∙ r2. Strøm I2 = Ia + I3. Strømmen I3 kan beregnes som i eksempel 1:

I3 = (220-80-40) / 20.000 = 0,005 A;

I2 = Ia + I3 = 0,01 + 0,005 = 0,015 A.

Spænding Ub = Ua + I2 ∙ r2 = 5 + 0,015 ∙ 6000 = 150 V.

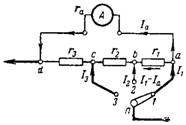
7. Beregn den kombinerede shunt for milliammeteret, så den ved forskellige positioner af kontakten har følgende måleområder: I1 = 10 mA; I2 = 30mA; I3 = 100mA. Shuntforbindelsesdiagrammet er vist i fig. 6. Enhedens indre modstand ra = 40 Ohm. Indre måleområde på milliammeter 2 mA.

Ris. 6.

Ved måling af strøm I≤2mA er shunten slået fra.

a) Ved måling af strømmen I = 10 mA er kontakten i position 1, og en strøm på 10-2 = 8 mA løber gennem alle shuntmodstandene. Spændingsfaldet over shuntmodstanden Ush og apparatet Ua mellem punkterne d og a skal være det samme

Ush = Ua;

(I1-la) ∙ (r1 + r2 + r3) = Ia ∙ ra;

0,008 ∙ (r1 + r2 + r3) = 0,002 ∙ 40.

b) Ved måling af strøm I2 = 30 mA er kontakten i position 2. Den målte strøm vil dele sig i punkt b. Ved fuld afbøjning af enhedens viser vil strømmen Ia = 2 mA passere gennem modstanden r1 og enheden ra.

Resten af ​​strømmen I2-Ia vil passere gennem modstandene r2 og r3. Strømmene vil skabe det samme spændingsfald over de to grene mellem punkterne d og b:

(I2-Ia) ∙ (r2 + r3) = Ia ∙ r1 + Ia ∙ ra;

(0,03-0,002) ∙ (r2 + r3) = 0,002 ∙ (r1 + 40).

c) På lignende måde vil vi udføre beregningen, når vi øger måleområdet til I3 = 100 mA. Strøm I3-Ia vil strømme gennem modstand r3 og strøm Ia gennem modstand r1, r2, ra. Spændingen i begge grene er den samme: (I3-Ia) ∙ r3 = Ia ∙ r1 + Ia ∙ r2 + Ia ∙ ra;

0,098 ∙ r3 = 0,002 ∙ (r1 + r2 + 40).

Vi opnåede tre ligninger med tre ukendte værdier af modstande r1, r2 og r3.

Vi ganger alle ligninger med 1000 og omregner dem:

r1 + r2 + r3 = 10;

14 ∙ (r2 + r3) -r1 = 40;

49 ∙ r3-r1-r2 = 40.

Lad os tilføje første og tredje ligning: 50 ∙ r3 = 50;

r3 = 50/50 = 1 ohm.

Lad os tilføje den første og anden ligning: 15 ∙ r2 + 15 ∙ r3 = 50;

15 ∙ r2 + 15 ∙ 1 = 50;

15 ∙ r2 = 35; r2 = 2,34 ohm.

Lad os erstatte de opnåede resultater i den første ligning: r1 + 35/15 + 1 = 10;

15 ∙ r1 + 35 + 15 = 150;

r1 = 100/15 = 6,66 ohm.

Rigtigheden af ​​beregningen kan kontrolleres ved at erstatte de opnåede modstandsværdier i ligningerne.