Spændingsfald

Begreber og formler

Ved hver modstand r, når strømmen I passerer, fremkommer en spænding U = I ∙ r, som normalt kaldes denne modstands spændingsfald.

Hvis der kun er én modstand r i kredsløbet, falder hele kildespændingen Ust på denne modstand.

Hvis kredsløbet har to modstande r1 og r2 forbundet i serie, så er summen af ​​spændingerne i modstandene U1 = I ∙ r1 og U2 = I ∙ r2, dvs. spændingsfald er lig med kildespændingen: Ust = U1 + U2.

Forsyningsspændingen er lig med summen af ​​spændingsfaldene i kredsløbet (Kirchhoffs 2. lov).

Eksempler på

1. Hvilket spændingsfald opstår over lampens glødetråd med modstand r = 15 Ohm, når strømmen I = 0,3 A passerer (fig. 1)?

Ris. 1.

Antallet af spændingsfald Ohms lov: U = I ∙ r = 0,3 ∙ 15 = 4,5 V.

Spændingen mellem punkt 1 og 2 på lampen (se diagrammet) er 4,5 V. Lampen lyser normalt, hvis mærkestrømmen løber igennem den, eller hvis der er en mærkespænding mellem punkt 1 og 2 (mærkestrømmen og spændingen er angivet på lampen).

2. To identiske pærer til en spænding på 2,5 V og en strøm på 0,3 A er seriekoblet og forbundet til et lommebatteri med en spænding på 4,5 V. Hvilket spændingsfald genereres ved terminalerne på de enkelte pærer (fig. 2) )) ?

Ris. 2.

Identiske pærer har samme modstand r. Når de er forbundet i serie, løber den samme strøm I gennem dem. Det følger heraf, at de vil have samme spændingsfald, summen af ​​disse spændinger skal være lig med kildespændingen U = 4,5 V. Hver pære har en spænding på 4 5:2 = 2,25V.

Du kan løse dette problem og sekventiel beregning. Vi beregner pærens modstand i henhold til dataene: rl = 2,5 / 0,3 = 8,33 Ohm.

Kredsløbsstrøm I = U / (2rl) = 4,5 / 16,66 = 0,27 A.

Spændingsfaldet over pæren U = Irl = 0,27 ∙ 8,33 = 2,25 V.

3. Spændingen mellem skinnen og køreledningen på sporvognslinjen er 500 V. Fire identiske lamper forbundet i serie bruges til belysning. Til hvilken spænding skal hver lampe (fig. 3) vælges?

Ris. 3.

Identiske lamper har lige store modstande, hvorigennem den samme strøm løber. Spændingsfaldet over lamperne vil også være det samme. Det betyder, at der for hver lampe vil være 500:4 = 125 V.

4. To lamper med en effekt på 40 og 60 W med en nominel spænding på 220 V er forbundet i serie og er forbundet til et netværk med en spænding på 220 V. Hvilket spændingsfald opstår over hver af dem (fig. 4)?

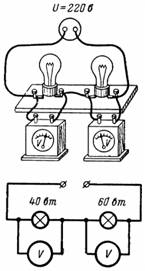
Ris. 4.

Den første lampe har en modstand r1 = 1210 Ohm, og den anden r2 = 806,6 Ohm (i opvarmet tilstand). Strømmen, der passerer gennem lamperne, er I = U / (r1 + r2) = 220 / 2016,6 = 0,109 A.

Spændingsfald i den første lampe U1 = I ∙ r1 = 0,109 ∙ 1210 = 132 V.

Spændingsfald i den anden lampe U2 = I ∙ r2 = 0,109 ∙ 806,6 = 88 V.

En lampe med en højere modstand har et større spændingsfald og omvendt. Glødetrådene i begge lamper er meget svage, men 40W-lampen er lidt stærkere end 60W-lampen.

5. For at spændingen på elmotoren D (fig. 5) skal være lig med 220 V, skal spændingen i begyndelsen af ​​den lange ledning (ved kraftværket) være mere end 220 V i værdi spændingsfald (tab) online. Jo større modstanden af ​​ledningen og strømmen i den, jo større spændingsfald langs linjen.

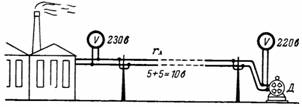Ris. 5.

I vores eksempel er spændingsfaldet i hver ledning af linjen 5 V. Så skal spændingen ved strømskinnerne på kraftværket være lig med 230 V.

6. Forbrugeren forsynes med et 80 V batteri med en strømstyrke på 30 A. For normal drift af forbrugeren er et 3 % spændingsfald i aluminiumtråde med et tværsnit på 16 mm2 tilladt. Hvad er den maksimale afstand fra batteriet til brugeren?

Tilladt spændingsfald i ledningen U = 3/100 ∙ 80 = 2,4 V.

Modstanden af ​​ledningerne er begrænset af det tilladte spændingsfald rpr = U / I = 2,4 / 30 = 0,08 Ohm.

Ved hjælp af formlen til bestemmelse af modstanden beregner vi længden af ​​ledningerne: r = ρ ∙ l / S, hvorfra l = (r ∙ S) / ρ = (0,08 ∙ 16) / 0,029 = 44,1 m.

Hvis brugeren er 22 m fra batteriet, vil spændingen i det være mindre end 80 V ved 3 %, dvs. lig med 77,6 V.

7. En telegraflinje på 20 km er lavet af ståltråd med en diameter på 3,5 mm. Returledningen erstattes af jording gennem metalskinne. Modstanden for overgangen mellem bus og jord er rz = 50 Ohm.Hvad skal batterispændingen være i begyndelsen af ​​ledningen, hvis modstanden af ​​relæet for enden af ​​ledningen er рп = 300 Ohm og relæstrømmen er I = 5 mA?

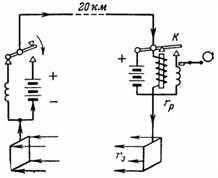
Ris. 6.

Tilslutningsdiagrammet er vist i fig. 6. Når telegrafkontakten trykkes på det sted, hvor signalet sendes, tiltrækker relæet ved modtagepunktet for enden af ​​ledningen ankeret K, som igen tænder optagerens spole med sin kontakt. Udgangsspændingen skal kompensere for spændingsfaldet i ledningen, modtagerelæet og jordingsskinnernes transiente modstande: U = I ∙ rl + I ∙ rр + I ∙ 2 ∙ rр; U = I ∙ (rр + рр + 2 ∙ rр).

Kildespændingen er lig med produktet af strømmen og kredsløbets samlede modstand.

Trådtværsnit S = (π ∙ d ^ 2) / 4 = (π ∙ 3,5 ^ 2) / 4 = 9,6 mm2.

Linjemodstand rl = ρ ∙ l / S = 0,11 ∙ 20.000 / 9,6 = 229,2 ohm.

Resulterende modstand r = 229,2 + 300 + 2 ∙ 50 = 629,2 Ohm.

Udgangsspænding U = I ∙ r = 0,005 ∙ 629,2 = 3,146 V; U≈3,2 V.

Spændingsfaldet i ledningen under passagen af ​​en strøm I = 0,005 A vil være: Ul = I ∙ rl = 0,005 ∙ 229,2 = 1,146 V.

Det relativt lave spændingsfald i ledningen opnås på grund af den lave værdi af strømmen (5 mA). Derfor skal der ved modtagepunktet være et følsomt relæ (forstærker), som tændes af en svag 5 mA puls og gennem sin kontakt tænder et andet, kraftigere relæ.

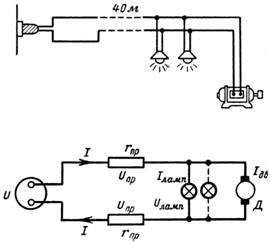
8. Hvor høj er spændingen af ​​lamperne i kredsløbet i fig. 28, når: a) motoren ikke er tændt; b) motoren starter; c) motoren kører.

Motoren og 20 lamper er tilsluttet en 110 V netforsyning Lamperne er designet til 110 V og 40 W. Motorens startstrøm er Ip = 50 A og dens mærkestrøm er In = 30 A.

Den indførte kobbertråd har et tværsnit på 16 mm2 og en længde på 40 m.

Fig. 7 og betingelserne for problemet, kan det ses, at motor- og lampestrømmen får linjespændingen til at falde, derfor vil belastningsspændingen være mindre end 110V.

Ris. 7.

U = 2 ∙ Ul + Ulamp.

Derfor er spændingen på lamperne Ulamp = U-2 ∙ Ul.

Det er nødvendigt at bestemme spændingsfaldet i ledningen ved forskellige strømme: Ul = I ∙ rl.

Modstand af hele linjen

2 ∙ rl = ρ ∙ (2 ∙ l) / S = 0,0178 ∙ (2 ∙ 40) / 16 = 0,089 Ohm.

Strømmen, der går gennem alle lamperne

20 ∙ Ilamp = 20 ∙ 40/110 = 7,27 A.

Netspændingsfald, når kun lamper er tændt (ingen motor),

2 ∙ Ul = Ilamp ∙ 2 ∙ rl = 7,27 ∙ 0,089 = 0,65 V.

Spændingen i lamperne er i dette tilfælde:

Ulamp = U-2 ∙ Ul = 110-0,65 = 109,35 V.

Når motoren startes, vil lamperne lyse mere svagt, da spændingsfaldet i ledningen er større:

2 ∙ Ul = (Ilamp + Idv) ∙ 2 ∙ rl = (7,27 + 50) ∙ 0,089 = 57,27 ∙ 0,089 = 5,1 V.

Minimumsspændingen på lamperne ved start af motoren vil være:

Ulamp = Uc-2, Ul = 110-5,1 = 104,9V.

Når motoren kører, er spændingsfaldet i ledningen mindre, end når motoren startes, men mere end når motoren er slukket:

2 ∙ Ul = (Ilamp + Inom) ∙ 2 ∙ rl = (7,27 + 30) ∙ 0,089 = 37,27 ∙ 0,089 = 3,32 V.

Spændingen på lamperne under normal motordrift er:

Ulamp = 110-3,32 = 106,68 V.

Selv et lille fald i lampernes spænding i forhold til den nominelle påvirker lysstyrken af ​​belysningen betydeligt.