Beregninger af magnetiske kredsløb

I elektriske maskiner og apparater er den magnetiske flux F koncentreret i det magnetiske kredsløb (ferromagnetiske kerne) og luftspalterne i dette magnetiske kredsløb. Denne bane af magnetisk flux kaldes et magnetisk kredsløb.

Et magnetisk kredsløb er som et elektrisk kredsløb. Den magnetiske flux Ф ligner en elektrisk strøm I, induktionen В ligner en strømtæthed, magnetiseringskraften (ns) Fн (H ∙ l = I ∙ ω) svarer til f.eks. etc. med

I det simpleste tilfælde har magnetkredsløbet det samme tværsnit overalt og er lavet af et homogent magnetisk materiale. For at bestemme n. med l ∙ ω, der kræves for at give den nødvendige induktion B, bestemmes den tilsvarende intensitet H ud fra magnetiseringskurven og ganges med middellængden af ​​magnetfeltlinjen l: H ∙ l = I ∙ ω = Fm.

Herfra bestemmes den nødvendige strøm I eller antallet af vindinger ω af spolen.

Et komplekst magnetisk kredsløb har normalt sektioner med forskellige sektioner og magnetiske materialer. Disse sektioner er normalt forbundet i serie, derfor passerer den samme magnetiske flux F gennem hver af dem.Induktion B i hver sektion afhænger af snittets tværsnit og beregnes for hvert snit separat ved formlen B = Φ∶S.

For forskellige induktionsværdier bestemmes intensiteten H ud fra magnetiseringskurven og multipliceres med den gennemsnitlige længde af strømledningen i den tilsvarende sektion af kredsløbet. Sammenfattende de enkelte værker får man den komplette n. c. magnetisk kredsløb:

Fm = I ∙ ω = H1 ∙ l1 + H2 ∙ l2 + H3 ∙ l3 + … som bestemmer magnetiseringsstrømmen eller antallet af spolevindinger.

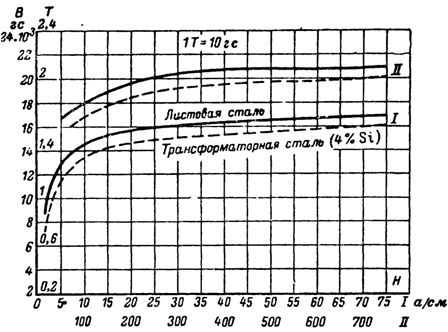
Magnetiseringskurver

Eksempler på

1. Hvad skal magnetiseringsstrømmen I være for en spole på 200 vindinger, så n. c. skabte i støbejernsringen en magnetisk flux Ф = 15700 Ms = 0,000157 Wb? Den gennemsnitlige radius af støbejernsringen er r = 5 cm, og diameteren af ​​dens snit er d = 2 cm (fig. 1).

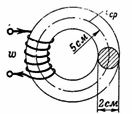
Ris. 1.

Snit af det magnetiske kredsløb S = (π ∙ d ^ 2) / 4 = 3,14 cm2.

Induktionen i kernen er: B = Φ∶S = 15700∶3,14 = 5000 G.

I MKSA-systemet er induktionen: B = 0,000157 Wb: 0,0000314 m2 = 0,5 T.

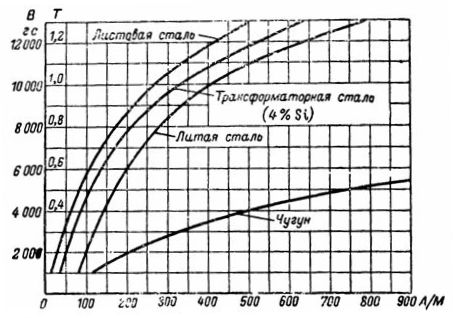
Ud fra magnetiseringskurven for støbejern finder vi den nødvendige styrke H lig med 750 A / m for B = 5000 G = 0,5 T. Magnetiseringsstyrken er lig med: I ∙ ω = H ∙ l = 235,5 Av.

Derfor er den nødvendige strøm I = (H ∙ l) / ω = 235,5 / 200 = 1,17 A.

2. Et lukket magnetisk kredsløb (fig. 2) er lavet af stålplader af en transformer. Hvor mange vindinger skal der være i en spole med en strøm på 0,5 A for at skabe en magnetisk flux i kernen Ф = 160000 Ms = 0,0016 Wb?

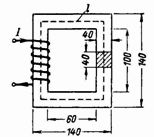
Ris. 2.

Kerneafsnit S = 4 ∙ 4 = 16 cm2 = 0,0016 m2.

Kerneinduktion B = F / S = 160000/16 = 10000 Gs = 1 T.

Ifølge transformatorstålets magnetiseringskurve finder vi for B = 10.000 Gs = 1 T intensiteten H = 3,25 A / cm = 325 A / m.

Den gennemsnitlige længde af magnetfeltlinjen er l = 2 ∙ (60 + 40) + 2 ∙ (100 + 40) = 480 = 0,48 m.

Magnetiseringskraft Fm = I ∙ ω = H ∙ l = 3,25 ∙ 48 = 315 ∙ 0,48 = 156 Av.

Ved en strøm på 0,5 A er antallet af vindinger ω = 156 / 0,5 = 312.

3. Det magnetiske kredsløb vist i fig. 3 svarer til det magnetiske kredsløb i det foregående eksempel, bortset fra at det har et luftgab på δ = 5 mm. Hvad skal n være. s. og spolestrømmen, således at den magnetiske flux er den samme som i det foregående eksempel, dvs. F = 160000 Ms = 0,0016 Wb?

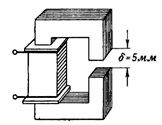
Ris. 3.

Det magnetiske kredsløb har to serieforbundne sektioner, hvis tværsnit er det samme som i det foregående eksempel, dvs. S = 16 cm2. Induktansen er også lig med B = 10000 G = 1 T.

Den gennemsnitlige længde af stålmagnetlinjen er lidt kortere: lс = 48-0,5 = 47,5 cm ≈0,48 m.

Den magnetiske spænding i denne sektion af det magnetiske kredsløb er Hc ∙ lc = 3,25 ∙ 48≈156 Av.

Feltstyrken i luftspalten er: Hδ = 0,8 ∙ B = 0,8 ∙ 10000 = 8000 A / cm.

Den magnetiske spænding i tværsnittet af luftspalten Hδ ∙ δ = 8000 ∙ 0,5 = 4000 Av.

Komplet n. c. er lig med summen af ​​magnetiske spændinger i individuelle sektioner: I ∙ ω = Hс ∙ lс + Hδ ∙ δ = 156 + 4000 = 4156 Av. I = (I ∙ ω) / ω = 4156/312 = 13,3 A.

Hvis den krævede magnetiske flux i det foregående eksempel blev leveret af en strøm på 0,5 A, så kræves der for et magnetisk kredsløb med et luftgab på 0,5 cm en strøm på 13 A for at opnå den samme magnetiske flux. Heraf kan det ses, at en luftspalte, selv ubetydelig i forhold til længden af ​​det magnetiske kredsløb, i høj grad øger den nødvendige n. v. og spolestrøm.

4. Transformatorens magnetiske flux er beregnet til at være F = 72000 Ms. Beregning af n er påkrævet.s.og magnetiseringsstrøm af primærviklingen med 800 vindinger. Der er et mellemrum δ = 0,2 mm i transformatorens kerne. Transformatorkernens dimensioner er vist i fig. 4. Tværsnit af kernen S = 2 ∙ 3​​= 6 cm2 (transformatorer med kerner af denne form kaldes pansrede).

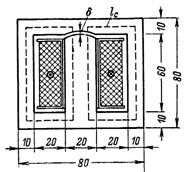
Ris. 4.

Kerne- og luftspaltinduktion B = F / S = 72000/6 = 12000 G.

Ifølge transformatorstålets magnetiseringskurve for B = 12000 G bestemmer vi intensiteten: Hc = 5 A / cm.

Den gennemsnitlige længde af magnetlinjen i stål er lс = 2 ∙ (6 + 3) = 18 cm.

Spænding i luftspalten Hδ = 0,8 ∙ B = 9600 A / cm.

Magnetiseringskraft I ∙ ω = Hc ∙ lc + Hδ ∙ δ = 5 ∙ 18 + 9600 ∙ 0,02 = 90 + 192 = 282 Av; I = (I ∙ ω) / ω = 282/800 = 0,35 A.

I den pansrede kerne opdeles den magnetiske flux i to dele, som er lukket langs sidestængerne, hvis tværsnit er S / 2, og den gennemsnitlige længde af den magnetiske linje er lc. Som et resultat er det magnetiske kredsløb fuldstændig analogt med det magnetiske kredsløb i en konventionel transformer med en fælles kerne S og en længde af strømledningen lc.

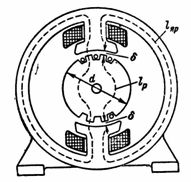
5. DC-maskinens magnetiske flux F = 1280000 Mks. Det magnetiske kredsløb indeholder et åg af støbt stål med en gennemsnitlig magnetisk linjelængde la = 80 cm, en rotor samlet af elektriske stålplader med en gennemsnitlig feltlængde lр = 18 cm og to luftspalter δ 0,2 cm hver. = 8 ∙ 20 cm2; rotor og polsektion Sр = 12 ∙ 20 cm2... Beregn n. s. og antallet af omdrejninger af polspolen, hvis den maksimale magnetiserende (spændende) strøm i den er 1 A (fig. 5).

Ris. 5.

Induktion i åget og stangen Bя = Ф / Sя = 1280000/160 = 8000 G.

Spændingen i åget og polen ifølge magnetiseringskurven for støbestål ved Bя = 8000 G er lig med:

H = 2,8 A/cm.

Magnetiseringskraften i sektionen af ​​åget HЯ ∙ la = 2,8 ∙ 80 = 224 Av.

Induktion i rotoren, stangen og luftspalten Br = Ф / Ср = 1280000/240 = 5333 G.

Spænding i en rotor lavet af stålplader ved Br = 5333 Gs Hrp = 0,9 A/cm,

og den magnetiske spænding af rotorsektionen Hр ∙ lр = 0,9 ∙ 18 = 16,2 Av.

Spænding i luftgabet Hδ = 0,8 ∙ Bδ = 0,8 ∙ 5333 = 4266,4 A / cm.

Den magnetiske spænding i tværsnittet af luftgabet Hδ ∙ 2 ∙ δ = 4266,4 ∙ 2 ∙ 0,2 = 1706,56 A.

Komplet n. c. lig med summen af ​​magnetiske spændinger i separate sektioner: I ∙ ω = Hя ∙ la + Hр ∙ lр + Hδ ∙ 2 ∙ δ; I ∙ ω = 224 + 16,2 + 1706,56 = 1946,76 Av.

Antallet af vindinger i de to polspoler ω = (I ∙ ω) / I = 1946,76 / 1≈2000.