Beregning af den resulterende modstand i serie-parallel forbindelse

Begreber og formler

En serie-parallel eller blandet forbindelse er en kompleks forbindelse af tre eller flere modstande. Den resulterende modstand af en blandet forbindelse beregnes i trin ved hjælp af formler til beregning af modstande i serie- og parallelforbindelser.

Eksempler på

1. Beregn serie-parallelforbindelsen af ​​tre modstande i henhold til diagrammet i fig. 1.

Udskift først de parallelforbundne modstande r2 og r3 med den resulterende modstand r (2-3):

r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 ohm.

Den resulterende modstand af hele kredsløbet er r = r1 + r (2-3) = 5 + 6,6 = 11,6 ohm.

Ris. 1.

2. Hvilken strøm der løber gennem kredsløbet (fig. 2) i de åbne og lukkede tilfælde knivafbryder P? Hvordan ændres spændingen over modstand r2 i begge tilfælde?

Ris. 2.

a) Kontakten er åben. Resulterende modstand af serieforbundne modstande r1 og r2

r (1-2) = r1 + r2 = 25 ohm.

Strøm I (1-2) = U / r (1-2) = 100/25 = 4 A.

Spændingsfald over modstand r2

U2 = I (1-2) ∙ r2 = 4 ∙ 5 = 20 V.

b) Kontakten er lukket. Resulterende modstand af modstande r1 og r3 forbundet parallelt

r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 ohm.

Den samlede modstand af hele kredsløbet er r = r (1-3) + r2 = 6,6 + 5 = 11,6 ohm.

Strøm I = U / r = 100 / 11,6 = 8,62 A.

Spændingsfaldet over modstanden r2 er i dette tilfælde lig med: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.

I det andet tilfælde steg strømmen som et resultat af tilslutning af den parallelle modstand R3. Mere aktuelt skaber mere spændingsfald ved modstand r2.

3. Hvad skal være yderligere modstand rd, så to lamper forbundet parallelt til en spænding på 120 V og en strøm på 0,2 A kan tilsluttes et netværk med en spænding på U = 220 V (fig. 3)?

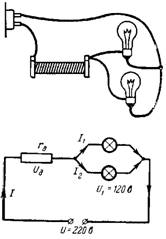
Ris. 3.

Spændingen i lamperne skal være lig med 120 V. Den resterende spænding (100 V) falder på den ekstra modstand rd. En strøm af to lamper I = 0,4 A løber gennem modstanden rd.

Ifølge Ohms lov rd = Ud / I = 100 / 0,4 = 250 Ohm.

4. Elektroniske lamper med en 1,2 V glødetråd og en glødetrådsstrøm på 0,025 og 0,05 A er forbundet i serie til en DC-kilde med spænding 4,5 V. Hvad skal den ekstra modstand rd og parallel modstand (shunt) til en lampe med lavere glødetrådsstrøm (fig. 4)?

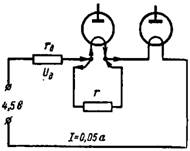
Ris. 4.

Modstandene i kredsløbet skal vælges således, at den anden lampes glødetrådsstrøm løber I = 0,05 A. Spændingen over glødetråden på de elektroniske lamper vil være 1,2 + 1,2 = 2,4 V. Trækker vi denne værdi fra batterispændingen, vi tag værdien af ​​spændingsfaldet over den ekstra modstand rd: Ud = 4,5-2,4 = 2,1 V.

Derfor er den ekstra modstand rd = (Ud) / I = 2,1 / 0,05 = 42 Ohm.

En glødetrådsstrøm på 0,05 A bør ikke strømme gennem glødetråden i det første vakuumrør. Halvdelen af ​​denne strøm (0,05-0,025 = 0,025 A) skal passere gennem shunten r. Shuntspændingen er den samme som lampens glødetråd, dvs. 1,2 V. Derfor er shuntmodstanden: r = 1,2 / 0,025 = 48 Ohm.

5. Hvad er den resulterende kredsløbsmodstand og strømmen i den i kredsløbet i fig. 5?

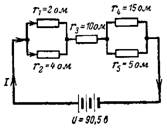
Ris. 5.

Lad os først bestemme den resulterende modstand af de parallelforbundne modstande:

r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 ohm;

r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 ohm.

Den resulterende kredsløbsmodstand er:

r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 ohm.

Den resulterende strøm ved spænding U = 90,5 V

I = U / r = 90,5 / 15,05 = 6 A.

6. Beregn den resulterende modstand af en kompleks serie-parallel forbindelse i kredsløbet i fig. 6. Beregn den resulterende strøm I, strøm I4 og spændingsfald over modstand r1.

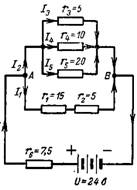
Ris. 6.

Resulterende konduktans af parallelforbundne modstande

1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;

r (3-4-5) = 20/7 = 2,85 ohm.

Kredsløbsmodstanden for r1 og r2 er:

r (1-2) = r1 + r2 = 15 + 5 = 20 ohm.

Den resulterende ledningsevne og modstand mellem punkt A og B er henholdsvis ens: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 ohm.

Den resulterende modstand af hele kredsløbet er r = rAB + r6 = 2,5 + 7,5 = 10 ohm.

Den resulterende strøm er I = U / r = 24/10 = 2,4 A.

Spændingen mellem punkt A og B er lig med kildespændingen U minus spændingsfaldet over modstanden r6

UAB = U-I ∙ r6 = 24-(2,4 ∙ 7,5) = 6V.

Modstanden r4 er forbundet med denne spænding, så strømmen gennem den vil være lig med:

I4 = UAB / r4 = 6/10 = 0,6A.

Modstande r1 og r2 har et fælles spændingsfald UAB, så strømmen gennem r1 er:

I1 = UAB / r (1-2) = 6/20 = 0,3 A.

Spændingsfald over modstand r1

Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.

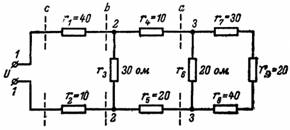
7. Hvad er den resulterende modstand og strøm i kredsløbet i fig. 7 hvis kildespændingen er U = 220 V?

Ris. 7.

Vi starter med kredsløbet placeret til højre for knudepunkter 3 og 3. Modstandene r7, r8, r9 er forbundet i serie, derfor

r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 ohm.

En modstand r6 er forbundet parallelt med denne modstand, så den resulterende modstand ved node 3 og 3 (afsnit a)

ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 ohm.

Modstande r4 og r5 er forbundet i serie med modstand ra:

r (4-5-a) = 10 + 20 + 16,36 = 46,36 ohm.

Resulterende modstand af knudepunkter 2 og 2 (afsnit b)

rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46,36 ∙ 30) / (46,36 + 30) = 1390,8 / 76, 36 = 18,28 ohm.

Den resulterende modstand af hele kredsløbet er r = r1 + rb + r2 = 40 + 18,28 + 10 = 68,28 ohm.

Den resulterende strøm er I = U / r = 220 / 68,28 = 3,8 A.