Beregning af shunten for amperemeteret

Begreber og formler

En shunt er en modstand, der er forbundet på tværs af amperemeterterminalerne (parallelt med instrumentets interne modstand) for at øge måleområdet. Den målte strøm I deles mellem måleshunt (rsh, Ish) og amperemeter (ra, Ia) omvendt proportional med deres modstande.

Shuntmodstand rsh = ra x Ia / (I-Ia).

For at øge måleområdet med n gange, skal shunten have en modstand rsh = (n-1) / ra

Eksempler på

1. Det elektromagnetiske amperemeter har indre modstand ra = 10 Ohm, og måleområdet er op til 1 A. Beregn shuntmodstanden rsh, så amperemeteret kan måle strøm op til 20 A (fig. 1).

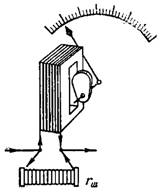
Ris. 1.

Den målte strøm på 20 A vil opdeles i en strøm Ia = 1 A, der vil strømme gennem amperemeteret og en strøm Ish, der vil strømme gennem shunten:

I = Ia + Ish.

Derfor strømmer strømmen gennem shunten, Ish = I-Ia = 20-1 = 19 A.

Den målte strøm I = 20 A skal deles i forholdet Ia: Ish = 1:19.

Det følger heraf, at grenmodstandene skal være omvendt proportional med strømmene: Ia: Ish = 1 / ra: 1 / rsh;

Ia: Ish = rsh: ra;

1:19 = rv: 10.

Shuntmodstand rsh = 10/19 = 0,526 Ohm.

Shuntmodstanden skal være 19 gange mindre end amperemetermodstanden ra, så strømmen Ish går igennem den, hvilket er 19 gange større end strømmen Ia = 1 A, der går gennem amperemeteret.

2. Det magnetoelektriske milliammeter har et non-shunt måleområde på 10 mA og en indre modstand på 100 Ohm. Hvilken modstand skal shunten have, hvis enheden skal måle strøm op til 1 A (fig. 2)?

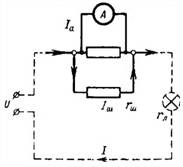
Ris. 2.

Ved fuld afbøjning af nålen vil strømmen Ia = 0,01 A passere gennem spolen på milliammeteret og gennem shunten Ish:

I = Ia + Ish,

hvorfra Ish = I-Ia = 1-0,99 A = 990 mA.

Strømmen 1 A vil blive opdelt i omvendt proportion til modstandene: Ia: Ish = rsh: ra.

Ud fra dette forhold finder vi shuntmodstanden:

10: 990 = rsh: 100; rsh = (10×100) / 990 = 1000/990 = 1.010 Ohm.

Ved fuld afbøjning af pilen vil strøm Ia = 0,01 A passere gennem enheden, strøm Ish = 0,99 A gennem shunten og strøm I = 1 A.

Ved måling af strømmen I = 0,5 A vil strømmen Ish = 0,492 A passere gennem shunten og strømmen Ia = 0,05 A vil passere gennem amperemeteret. Pilen afviger til halv skala.

For enhver strøm fra 0 til 1 A (med den valgte shunt) er strømmene i grenene opdelt i forholdet ra: rsh, dvs. 100: 1,01.

3. Amperemeteret (fig. 3) har en indre modstand rа = 9,9 Ohm, og modstanden af ​​dets shunt er 0,1 Ohm. Hvad er forholdet mellem den målte strøm på 300 A i enheden og shunten?

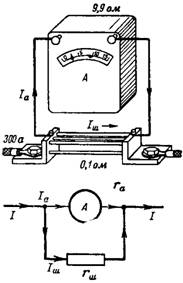
Ris. 3.

Vi vil løse problemet ved at bruge Kirchhoffs første lov: I = Ia + Ish.

Også Ia: Ish = rsh: ra.

Herfra

300 = Ia + Ish;

Ia: Ish = 0,1: 9,9.

Fra den anden ligning får vi den aktuelle Ia og erstatter den i den første ligning:

Ia = 1/99xIsh;

300 = 1 / 99xIsh + Ish;

Ishx (1 + 1/99) = 300;

Ishx100 / 99 = 300;

Ish = 300 / 100 × 99 = 297 A.

Strømmen i enheden Ia = I-Ish = 300-297 = 3 A.

Ud fra den samlede målte strøm vil strøm Ia = 3 A passere gennem amperemeteret, og Ish = 297 A gennem shunten.

Amperemeter shunt

4. Et amperemeter, hvis indre modstand er 1,98 Ohm, giver en fuld afbøjning af pilen ved en strøm på 2 A. Det er nødvendigt at måle strømmen op til 200 A. Hvilken modstand skal en shunt koblet parallelt til enhedens terminaler har?

I denne opgave øges måleområdet med en faktor 100: n = 200/2 = 100.

Den nødvendige modstand af shunten rsh = rа / (n-1).

I vores tilfælde vil shuntmodstanden være: rsh = 1,98 / (100-1) = 1,98 / 99 = 0,02 Ohm.