Trækkraft af elektromagneter
Den kraft, hvormed en elektromagnet tiltrækker ferromagnetiske materialer, afhænger af den magnetiske flux F eller tilsvarende af induktionen B og tværsnitsarealet af elektromagneten S.
Elektromagnetens trykkraft bestemmes af formlen
F = 40550 ∙ B ^ 2 ∙ S,
hvor F er elektromagnetens trykkraft, kg (kraften måles også i newton, 1 kg = 9,81 N eller 1 N = 0,102 kg); B — induktion, T; S er tværsnitsarealet af elektromagneten, m2.
Eksempler på
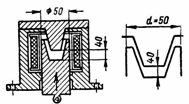
1. Vandhanens elektromagnet er et magnetisk kredsløb (fig. 1). Hvad er løftekraften af en hestesko-kran-elektromagnet, hvis den magnetiske induktion er B = 1 T, og tværsnitsarealet af hver pol af elektromagneten er S = 0,02 m2 (fig. 1, b)? Forsøm virkningen af mellemrummet mellem elektromagneten og armaturet.
Ris. 1. Løfte elektromagnet
F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.
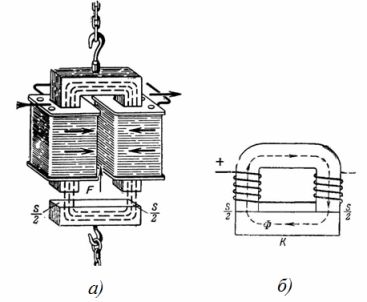
2. En cirkulær stålelektromagnet har målene vist i fig. 2, a og b. Elektromagnetens løftekraft er 3 T. Bestem tværsnitsarealet af elektromagnetkernen, n. p. og antallet af vindinger af spolen ved en magnetiseringsstrøm I = 0,5 A.
Ris. 2. Rund elektromagnet
Den magnetiske flux passerer gennem den cirkulære indre kerne og vender tilbage gennem den cylindriske krop. Tværsnitsarealerne af kernen Sc og foringsrøret Sk er omtrent det samme, derfor er induktionsværdierne i kernen og foringsrøret praktisk talt de samme:
Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,
Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;
S = Sc + Sk = 0,24995 m2 ≈0,25 m2.
Den nødvendige induktion i elektromagneten bestemmes af formlen F = 40550 ∙ B ^ 2 ∙ S,
hvor B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.
Spændingen ved denne induktion findes på magnetiseringskurven for støbestålet:
H = 180 A/m.
Den gennemsnitlige længde af marklinjen (fig. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.
Magnetiseringskraft I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; I = (I ∙ ω) / I = 154,8 / 0,5 = 310 A.
Faktisk n. s, det vil sige strømmen og antallet af omdrejninger, skal være mange gange større, da der er et uundgåeligt luftgab mellem elektromagneten og ankeret, hvilket markant øger magnetkredsløbets magnetiske modstand. Derfor skal der tages højde for luftgabet ved beregning af elektromagneterne.
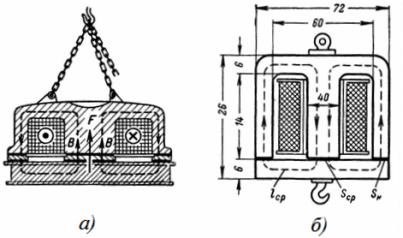
3. Elektromagnetens spole til vandhanen har 1350 omdrejninger, gennem den løber en strøm I = 12 A. Elektromagnetens dimensioner er vist i fig. 3. Hvilken vægt løfter elektromagneten i en afstand af 1 cm fra armaturet, og hvilken vægt kan den holde efter tyngdekraften?
Ris. 3. Elektromagnetisk spole
Det meste af N. med I ∙ ω bruges på at lede magnetisk flux gennem luftgabet: I ∙ ω≈Hδ ∙ 2 ∙ δ.
Magnetiseringskraft I ∙ ω = 12 ∙ 1350 = 16200 A.
Da H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, så er Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.
Derfor er 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, dvs. B = 1,012T.
Vi antager, at induktionen er B = 1 T, da en del af n. c. I ∙ ω bruges på at lede magnetisk flux i stål.
Lad os kontrollere denne beregning ved hjælp af formlen I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.
Den gennemsnitlige længde af den magnetiske linje er: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.
Intensiteten Hc ved B = 1 T (10000 Gs) bestemmes ud fra magnetiseringskurven:
Hc = 260 A / m. I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Gns.
Magnetiseringskraften I ∙ ω = 16114 Av skaber en induktion B = 1 T er praktisk talt lig med den givne n. v. I ∙ ω = 16200 Av.
Det samlede tværsnitsareal af kernen og keglen er: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.
Elektromagneten vil tiltrække en ladning med vægt F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg fra en afstand på 1 cm.
Da luftgabet praktisk talt forsvinder, efter at ankeret er tiltrukket, kan elektromagneten modstå en meget større belastning. I dette tilfælde er hele n. c. I ∙ ω bruges kun på at lede magnetisk flux i stål, derfor I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.
Ved en sådan spænding er stålet praktisk talt mættet, og induktionen i det er cirka 2 T. Elektromagneten tiltrækker ankeret med en kraft F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.
4. Signal (blinker) relæet består af en pansret elektromagnet 1 med en rund kerne og et anker 2 af ventiltypen, som efter at have tilført strøm til elektromagneten tiltrækker og udløser blinket 3, som åbner signalcifferet (fig. 4).
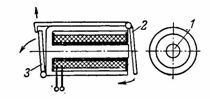
Ris. 4. Panserelektromagnet
Magnetiseringsstyrken er I ∙ ω = 120 Av, luftgabet er δ = 0,1 cm, og det samlede tværsnitsareal af elektromagneten er S = 2 cm2. Estimer relæets trækkraft.
Induktansen B bestemmes ved successive tilnærmelser ved hjælp af ligningen I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.
Lad n. c. Hc ∙ lc er 15 % I ∙ ω, dvs. 18 Av.
Så I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102/0,2 = 510 A/cm = 51000 A/m.
Derfor finder vi induktion B:
Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0,0637 T.
Efter at have erstattet værdien B i formlen F = 40550 ∙ B ^ 2 ∙ S, får vi:
F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.
5. DC-bremsemagneten (fig. 5) har et stempelanker med et tilspidset stop. Afstanden mellem ankeret og kernen er 4 cm Arbejdsdiameteren (kerner med cirkulær kontaktflade) d = 50 mm. Armaturet trækkes ind i spolen med en kraft på 50 kg. Længden af den midterste kraftlinje lav = 40 cm Bestem n. s. og spolestrømmen, hvis der er 3000 vindinger.
Ris. 5. DC-bremsemagnet
Arealet af elektromagnetens arbejdssektion er lig med arealet af en cirkel med en diameter d = 5 cm:
S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.
Den induktion B, der kræves for at skabe en kraft F = 50 kg, findes ud fra ligningen F = 40550 ∙ B ^ 2 ∙ S,
hvor B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.
Magnetiseringskraft I ∙ ω = Hс ∙ lс + Hδ ∙ δ.
Vi bestemmer magnetiseringsstyrken for stål Hc ∙ lc på en forenklet måde, baseret på det faktum, at den er 15 % I ∙ ω:
I ∙ ω = 0,15 ∙ I ∙ ω + Hδ ∙ δ; 0,85 ∙ I ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30.000 Gns.
Magnetiseringsstrøm I = (I ∙ ω) / ω = 30000/3000 = 10 A.