Teori om automater, endelige automater
Strukturen, designet, funktionsprincippet for forskellige maskiner er i vid udstrækning bestemt af dets funktionelle formål. Skelne mellem teknologiske, transport-, computer-, militær- og andre maskiner. Hele automatiske komplekser designet til at udføre komplekse teknologiske processer er bredt introduceret i forskellige industrier. Automater er designet og bygget, der udfører forskellige logiske funktioner (logiske maskiner).
Teori om automater — kybernetik sektion, som opstod under indflydelse af kravene til teknologien til digitale computere og styremaskiner. Diskrete automater studeret i automatteori er abstrakte modeller af virkelige systemer (både tekniske og biologiske), der behandler diskret (digital) information på diskrete tidstrin.
Automateteori er baseret på præcise matematiske begreber, der formaliserer intuitive ideer om automatens funktion (adfærd) og om dens struktur (indre struktur).
I dette tilfælde forstås informationstransformation altid som en operation, der transformerer inputsekvenser sammensat af bogstaver fra inputalfabetet til outputsekvenser sammensat af bogstaver fra outputalfabetet.
Apparatet for matematisk logik, algebra, sandsynlighedsteori, kombinatorik og grafteori er meget brugt.
Problemet med teorien om automater i nogle af dens dele (strukturel teori om automater) voksede fra teorien om relæ-kontaktkredsløb, som begyndte at tage form i slutningen af 1930'erne. inklusive metoder til logisk algebra.

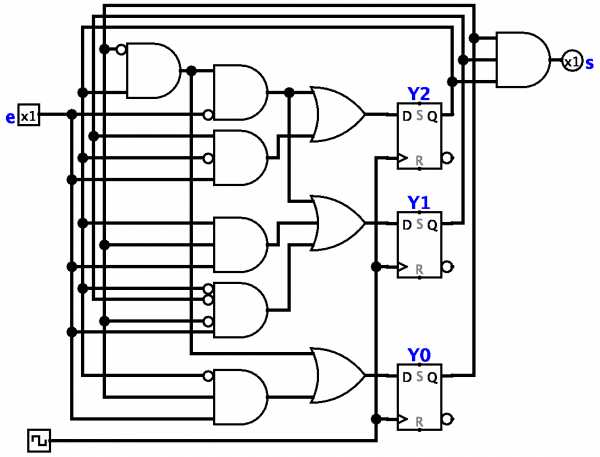
I den strukturelle teori om automater studeres forskellige typer skemaer, designet til at beskrive, hvordan en kompleks automat er skabt af enklere komponenter (elementer) korrekt forbundet i et system.
En anden retning, kaldet den abstrakte teori om automater, studerer opførsel af automater (det vil sige arten af transformationen af information udført af dem), mens den abstraherer fra detaljerne i deres interne struktur, og opstod i 1950'erne.
Inden for rammerne af den abstrakte teori om automater er indholdet af begreberne "automat" og "maskine" i det væsentlige udtømt af standardbeskrivelsen af den transformation af information, som udføres af en automat. En sådan transformation kan være deterministisk, men den kan også være sandsynlig.
De mest undersøgte er deterministiske maskiner (automater), som inkluderer endelige automater - hovedobjektet for undersøgelsen i teorien om automater.
En finite state-maskine er karakteriseret ved en begrænset mængde hukommelse (antallet af interne tilstande) og defineres ved hjælp af en overgangsfunktion.Med en vis rimelig idealisering kan alle moderne matematiske maskiner og endda hjernen, ud fra deres funktionssynspunkt, betragtes som endelige automater.
Udtrykkene "sekventiel maskine", "Milly automat", "Moore automaton" bruges i litteraturen (og ikke ensartet af alle forfattere) som synonymer til udtrykket "endelig automat" eller for at understrege visse træk i overgangsfunktionerne for en endelig automat.
Automata med ubegrænset hukommelse er en Turing-maskine, der er i stand til at udføre (potentielt) enhver effektiv informationstransformation. Begrebet "Turing-maskine" opstod tidligere end begrebet "finite state machine" og er hovedsageligt studeret i teorien om algoritmer.
Abstrakt automatteori er tæt beslægtet med velkendte algebraiske teorier, for eksempel semigruppeteori. Fra et anvendt synspunkt er resultaterne, der karakteriserer transformationen af information i en automat med hensyn til hukommelsesstørrelse, af interesse.
Dette er for eksempel tilfældet i problemer med eksperimenter på automater (værker af E.F. Moore, etc.), hvor en eller anden information om automatens overgangsfunktioner eller om kapaciteten af dens hukommelse hentes fra resultaterne af eksperimenter.
En anden opgave er at beregne perioderne for outputsekvenserne, baseret på den tilgængelige information om automatens hukommelsesstørrelse og perioderne for inputsekvenserne.
Af stor betydning er udviklingen af metoder til at minimere hukommelsen af finite state maskiner og studere deres adfærd i tilfældige miljøer.
I abstrakt automatteori er synteseproblemet følgende.Med hensyn til et klart formaliseret sprog er betingelserne skrevet for den designede automats opførsel (for den begivenhed, der er repræsenteret i automaten). I dette tilfælde er det nødvendigt at udvikle metoder, der i henhold til hver skriftlig betingelse:
1) finde ud af, om der eksisterer en sådan tilstandsmaskine, at den information, der transformeres af den, opfylder denne betingelse;
2) hvis ja, så konstrueres overgangsfunktionerne for en sådan finite state-maskine, eller dens hukommelsesstørrelse estimeres.
Løsningen af synteseopgaven i en sådan formulering forudsætter den foreløbige oprettelse af et bekvemt sprog til registrering af driftsbetingelserne for en automat med praktiske algoritmer til overgangen fra optagelse til transitive funktioner.
I den strukturelle teori om automater består synteseproblemet i at konstruere en kæde af elementer af en given type, der realiserer en endelig automat givet af dens overgangsfunktioner. I dette tilfælde angiver de normalt et eller andet optimalitetskriterium (for eksempel minimumsantallet af elementer) og søger at opnå en optimal ordning.
Som det senere viste sig, betyder det, at nogle af de metoder og koncepter, der er udviklet tidligere i forhold til relæ-kontaktkredsløb, er anvendelige på kredsløb af en anden type.
I forbindelse med udviklingen af elektroniske teknologier er ordningerne mest udbredt af funktionelle elementer (logiske netværk). Et særligt tilfælde af logiske netværk er abstrakte neurale netværk, hvis elementer kaldes neuroner.
Mange syntesemetoder er blevet udviklet, afhængigt af typen af kredsløb og transformationen af information, som de er beregnet til (Syntese af relæenheder).
Se -Minimering af kombinationskredsløb, Carnot-kort, kredsløbssyntese
Finite state maskine — en matematisk model af et kontrolsystem med en fast (ikke i stand til at øges under drift) hukommelsesstørrelse.
Konceptet med en endelig tilstandsmaskine er en matematisk abstraktion, der karakteriserer de generelle karakteristika for et sæt kontrolsystemer (for eksempel en multi-loop relæenhed). Alle sådanne systemer har fælles træk, som det er naturligt at acceptere som definitionen af en endelig automat.
Hver færdig automat har en indgang udsat for ydre påvirkninger og indre elementer. For både input og interne elementer er der et fast antal diskrete tilstande, som de kan tage.
Ændringen i tilstandene for input og interne elementer sker på diskrete tidspunkter i tiden, intervallerne mellem hvilke kaldes kryds. Den interne tilstand (tilstanden af det interne) ved slutningen af båndet bestemmes udelukkende af den interne tilstand og tilstanden af input ved begyndelsen af båndet.
Alle andre definitioner af en endelig automat kan reduceres til denne karakteristik, især definitioner, der antager, at en endelig automat har et output, der afhænger af den interne tilstand af automaten på et givet tidspunkt.
Med hensyn til en sådan karakteristik er arten af dens input og interne tilstande irrelevant for beskrivelsen af en komplet automat. I stedet for input og tilstande kan du bare se på deres tal i en tilfældig nummerering.
Tilstandsmaskinen vil blive indstillet, hvis afhængigheden af dens interne tilstandsnummer af det tidligere interne tilstandsnummer og det tidligere inputtilstandsnummer er specificeret. Sådan en opgave kan være i form af et finalebord.
En anden almindelig måde at definere en komplet automat er konstruktionen af den såkaldte overgangsdiagrammer. Inputtilstande kaldes ofte blot input, og interne tilstande er simpelthen tilstande.
En finite state-maskine kan være en model af både tekniske anordninger og nogle biologiske systemer. Automater af den første type er for eksempel relæenheder og forskellige elektroniske computere, inkl. programmerbare logiske controllere.
I tilfælde af en relæenhed spilles rollen som inputtilstande af kombinationer af tilstande af de følsomme elementer i relæanordningen (hver kombination af sådanne tilstande er en «kompleks tilstand», karakteriseret ved en indikation af alle de følsomme elementer af disse diskrete tilstande, som de har i et givet øjeblik). Tilsvarende fungerer kombinationer af tilstande af mellemelementer i en relæanordning som interne tilstande.
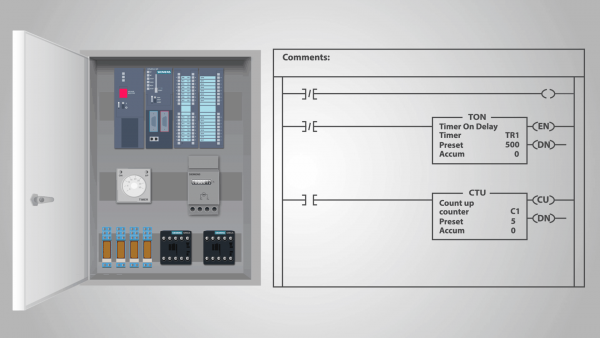
En programmerbar logisk controller (PLC) er et eksempel på en relæhandlingsenhed, der kan kaldes en stand-alone tilstandsmaskine.
Faktisk, når først programmet er blevet indtastet i PLC'en, og controlleren er begyndt at beregne, er det ikke udsat for ydre påvirkninger, og hver efterfølgende tilstand er fuldstændig bestemt af dens tidligere tilstand. Vi kan antage, at inputtet har samme tilstand i hver urcyklus.
Omvendt kaldes enhver finite state-maskine, der har den eneste mulige input-tilstand, naturligvis autonom, da det ydre miljø i dette tilfælde ikke bærer nogen information, der styrer dets adfærd.
Se også:
Brugen af mikroprocessorsystemer i elektroteknik på eksemplet med brugen af PLC