Beregning af kondensatorkapacitans

Kapacitans C er kondensatorens kapacitet til at acceptere (lagre og holde) mængden af ​​elektricitet Q i ampere-sekunder eller ladningen Q i vedhæng. Hvis man fortæller et legeme, for eksempel en bold, en elektrisk ladning (elektricitetsmængde) Q, så vil et elektroskop, der er forbundet mellem dette legeme og jorden, vise en spænding U (fig. 1). Denne spænding er proportional med ladningen og afhænger også af kroppens form og størrelse.

Forholdet mellem ladning Q og spænding U er udtrykt ved formlen Q = C ∙ U.

Proportionalitetskonstanten C kaldes kroppens kapacitans. Hvis kroppen har form som en kugle, er kroppens kapacitans proportional med kuglens r radius.

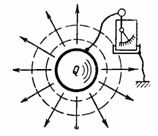
Ris. 1.

Måleenheden for kapacitans er farad (F).

Kroppen har en kapacitans på 1 F, når en ladning på 1 k frembringer en spænding på 1 V. mellem den og jorden. Farads er en meget stor måleenhed, så mindre enheder bruges i praksis: microfarad (μF), nanofarad (nF) og picofarad (pF)...

Disse enheder er forbundet med følgende forhold: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

Kapacitansen af ​​en kugle med en radius på 1 cm er 1,1 pF.

Ikke kun en isoleret krop kan akkumulere ladning, men også en speciel enhed kaldet en kondensator. En kondensator består af to eller flere plader (plader), der er adskilt af et dielektrikum (isolering).

I fig. 2 viser et kredsløb med en jævnstrømskilde forbundet til en kondensator. Når den er tændt, dannes en positiv ladning +Q i kondensatorens højre plade og en negativ ladning -Q i venstre plade. I løbet af kondensator ladning en strøm løber gennem kredsløbet, som stopper efter afslutningen af ​​opladningen; så vil spændingen over kondensatoren være lig med e. etc. c. kilde U. Ladningen på kondensatorpladen, spænding og kapacitans hænger sammen med forholdet Q = C ∙ U. I dette tilfælde dannes et elektrostatisk felt i kondensatorens dielektrikum.

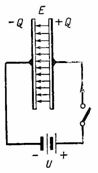
Ris. 2.

Kapaciteten af ​​en kondensator med et luftdielektrikum kan beregnes ved formlen C = S / (4 ∙ π ∙ d) ∙ 1.11, pF, hvor S er arealet af en plade, cm2; d er afstanden mellem pladerne, cm; C er kondensatorens kapacitans, pF.

Kapaciteten af ​​en kondensator bestående af n plader (fig. 3) er lig med: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

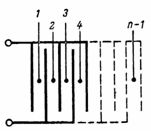
Ris. 3.

Hvis rummet mellem pladerne fyldes med et andet dielektrikum, for eksempel papir, vil kondensatorens kapacitans stige med en faktor ε. Når der bruges papirisolering, øges kapaciteten 3 gange, med glimmerisolering - 5-8 gange, med glas - 7 gange osv. Værdien af ​​ε kaldes dielektrikumets dielektriske konstant.

Den generelle formel til at bestemme kapacitansen af ​​en kondensator med dielektrisk konstant ε (epsilon) er: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1,11, pF.

Denne formel er nyttig til beregning af små variable kondensatorer til radioer.Den samme formel kan repræsenteres som: C = (ε_0 ∙ ε ∙ S) / d, hvor ε_0 er den dielektriske konstant eller den dielektriske konstant for vakuumet (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε er dielektrikumets dielektriske konstant.

I denne formel udskiftes dimensionerne i meter, og kapacitansen opnås i farad.

Eksempler på

1. Hvad er kapaciteten af ​​planeten Jorden, hvis radius er r = 6378 km?

Da kapacitansen af ​​en kugle med en radius på 1 cm er lig med 1,11 pF, er jordens kapacitans: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (Kapaciteten af ​​en kugle på størrelse med vores planet er relativt lille. Små elektrolytiske kondensatorer har denne kapacitet).

2. Bestem kapacitansen af ​​en kondensator bestående af to plader, som hver har et areal S = 120 cm2.

Pladerne er adskilt af et luftlag med en tykkelse på d = 0,5 cm, C = S / (4 ∙ π ∙ d) ∙ 1,11 = (120 ∙ 1,11) / (4 ∙ π ∙ 0,5) = 21,20 pF ...

3. Bestem kondensatorens kapacitans med dataene givet i det foregående eksempel, hvis mellemrummet mellem pladerne er fyldt med vokspapir med en dielektrisk konstant ε = 4, glas (ε = 7), elektrisk pap (ε = 2) glimmer (e = 8).

En vokspapirkondensator har en kapacitans C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.

Kapacitansen af ​​en glaskondensator er C = 7 ∙ 21,2 = 148,4 pF.

Kapacitansen af ​​papkondensatoren er C = 2 ∙ 21,2 = 42,3 pF.

Kapacitansen af ​​glimmerkondensatoren er C = 8 ∙ 21,2 = 169,6 pF.

4. Hvad er kapacitansen af ​​en luftroterende kondensator til en radiomodtager bestående af 20 plader med et areal på 20 cm2, hvis afstanden mellem pladerne er 0,06 cm (fig. 149)?

C = (n-1) ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1,11) / (4 ∙ π ∙ 0,06) = 559, 44 pF.

Kondensatoren vist i fig.3, består af separate simpleste kondensatorer med to plader, hvis antal er lig med n-1.

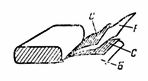
5. En papirkondensator med kapacitans C = 2 μF består af to strimler stanniol C og to strimler af et dielektrikum lavet af vokspapir B med en dielektrisk konstant ε = 6. Vokspapirets tykkelse er d = 0,1 mm. De foldede strimler rulles sammen, ledningerne er lavet af stålpladerne. Bestem længden af ​​kondensatorstålstrimlen, hvis dens bredde er 4 cm (fig. 4).

Ris. 4.

Først bestemmer vi arealet af en strimmel med formlen C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, hvorfra S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2.000.000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.

Længden af ​​hver strimmel er l = 37680/4 = 9420 cm = 94,2 m.