Beregning af varmelegemet

For at bestemme en af ​​hovedparametrene for varmeelementets ledning - diameter d, m (mm), anvendes to beregningsmetoder: i henhold til den tilladte specifikke overfladeeffekt PF og ved hjælp af tabellen over aktuelle belastninger.

Tilladt specifik overfladeeffekt PF= P⁄F,

hvor P er effekten af ​​trådvarmeren, W;

F = π ∙ d ∙ l — varmelegemeareal, m2; l — trådlængde, m.

Efter den første metode

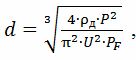
hvor ρd — elektrisk modstand af trådmaterialet ved faktisk temperatur, Ohm • m; U er varmetrådsspændingen, V; PF — tilladte værdier for specifik overfladeeffekt for forskellige varmeapparater:

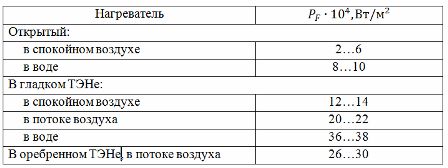
Den anden metode bruger en tabel over aktuelle belastninger (se tabel 1), der er kompileret ud fra eksperimentelle data. For at bruge den angivne tabel er det nødvendigt at bestemme den beregnede varmetemperatur Tp relateret til den faktiske (eller tilladte) temperatur på lederen Td ved forholdet:

Tr = Km ∙ Ks ∙ Td,

hvor Km er installationsfaktoren under hensyntagen til forringelsen af ​​varmelegemets køleforhold på grund af dets konstruktion; Kc er den omgivende faktor i betragtning af forbedringen af ​​varmerens kølebetingelser sammenlignet med et stationært luftmiljø.

For et varmeelement lavet af tråd snoet i en spiral, Km = 0,8 … 0,9; det samme, med en keramisk base Km = 0,6 ... 0,7; for en ledning af varmeplader og nogle varmeelementer Km = 0,5 ... 0,6; for en leder fra et elektrisk gulv, jord og varmeelementer Km = 0,3 ... 0,4. En mindre værdi på Km svarer til et varmelegeme med en mindre diameter, en større værdi til en større diameter.

Ved drift under andre forhold end fri konvektion tages Kc = 1,3 … 2,0 for varmeelementer i luftstrømmen; for grundstoffer i stille vand Kc = 2,5; i vandstrømmen — Kc = 3,0 … 3,5.

Hvis spændingen Uph og effekten Pf for fremtidens (designede) varmelegeme er indstillet, så er dens nuværende (pr. fase)

Iph = Pph⁄Uph

I henhold til den beregnede værdi af varmelegemets strøm for den nødvendige beregnede temperatur af dens opvarmning i henhold til tabel 1 findes den nødvendige diameter af nichromtråden d og den nødvendige længde af tråden, m, til fremstilling af varmelegemet er beregnet:

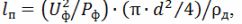
hvor d er den valgte tråddiameter, m; ρd er lederens specifikke elektriske modstand ved den aktuelle varmetemperatur, Ohm • m,

ρd = ρ20 ∙ [1 + αp ∙ (Td-20)],

hvor αр — temperaturkoefficient for modstand, 1/OS.

For at bestemme parametrene for nichromspiralen skal du tage den gennemsnitlige diameter af vindingerne D = (6 … 10) ∙ d, spiralens stigning h = (2 … 4) ∙ d,

antal omgange

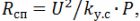
helixlængde lsp = h ∙ n.

Ved beregning af varmeelementerne skal det huskes, at modstanden af ​​spiraltråden efter tryk på varmeelementet

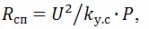
hvor k (y.s) er en koefficient, der tager højde for reduktionen i spiralens modstand; ifølge eksperimentelle data, k (s) = 1,25. Det skal også tages i betragtning, at den specifikke overfladeeffekt af spiraltråden er 3,5 ... 5 gange større end den specifikke overfladeeffekt af det rørformede varmeelement.

I praktiske beregninger af varmeelementet skal du først bestemme temperaturen på dets overflade Tp = To + P ∙ Rt1,

hvor det er den omgivende temperatur, ° C; P er varmeelementets effekt, W; RT1 — termisk modstand ved røret — medium grænseflade, ОC / W.

Derefter bestemmes viklingens temperatur: Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

hvor Rt2 er den termiske modstand af rørvæggen, ОC / W; RT3 — termisk modstand af fyldstoffet, ОC / W; Rp1 = 1⁄ (α ∙ F), hvor α er varmeoverførselskoefficienten, W / (m ^ 2 • ОС); F - varmelegemets areal, m2; Rt2 = δ⁄ (λ ∙ F), hvor δ er vægtykkelsen, m; λ — væggens varmeledningsevne, W / (m • ОС).

For mere information om varmeelementernes enhed, se her: Varmeelementer. Apparat, valg, drift, tilslutning af varmeelementer

Tabel 1. Tabel over aktuelle belastninger

Eksempel 1. Beregn det elektriske varmelegeme i form af en trådspiral i henhold til den tilladte specifikke overfladeeffekt PF.

Tilstand.Varmereffekt P = 3,5 kW; forsyningsspænding U = 220 V; trådmateriale — nichrome Х20Н80 (en legering af 20 % krom og 80 % nikkel), derfor den specifikke elektriske modstand af ledningen ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; temperaturkoefficient for modstand αр = 16 ∙ 10 ^ (- 6) 1 /ОС; spiralen er åben, i metallisk form, arbejdstemperaturen for spiralen er Tsp = 400 ОC, PF= 12 ∙ 10 ^ 4 W / m2. Bestem d, lp, D, h, n, lp.

Svar. Spolemodstand: R = U ^ 2⁄P = 220 ^ 2⁄3500 = 13,8 ohm.

Specifik elektrisk modstand ved Tsp = 400 OS

ρ400 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (400-20)] = 1,11 ∙ 10 ^ (- 6) Ohm • m.

Find diameteren på ledningen:

Fra udtrykket R = (ρ ∙ l) ⁄S får vi l⁄d ^ 2 = (π ∙ R) ⁄ (4 ∙ ρ), hvorfra ledningens længde

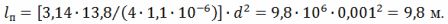
Den gennemsnitlige diameter af spiraldrejningen er D = 10 ∙ d = 10 ∙ 0,001 = 0,01 m = 10 mm. Spiralstigning h = 3 ∙ d = 3 ∙ 1 = 3 mm.

Antallet af drejninger i spiralen

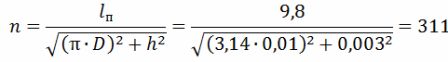
Helixens længde er lsp = h ∙ n = 0,003 ∙ 311 = 0,933 m = 93,3 cm.

Eksempel 2. Strukturelt beregne ledningsmodstandsvarmeren ved bestemmelse af ledningsdiameteren d ved hjælp af tabellen over strømbelastninger (se tabel 1).

Tilstand. Trådvarmereffekt P = 3146 W; forsyningsspænding U = 220 V; trådmateriale — nichrome Х20Н80 ρ20 = 1,1 ∙ 10 ^ ( — 6) Ohm • m; αp = 16 ∙ 10 ^ (- 6) 1 / ℃; åben helix placeret i luftstrømmen (Km = 0,85, Kc = 2,0); tilladelig driftstemperatur for lederen Td = 470 ОС.

Bestem diameteren d og længden af ​​tråden lp.

Svar.

Tr = Km ∙ Ks ∙ Td = 0,85 ∙ 2 ∙ 470 OS = 800 OS.

Designvarmerstrømmen I = P⁄U = 3146⁄220 = 14,3 A.

Ifølge tabellen over strømbelastninger (se tabel 1) ved Tр = 800 ОС og I = 14,3 A finder vi diameteren og tværsnittet af ledningen d = 1,0 mm og S = 0,785 mm2.

Trådlængde lp = (R ∙ S) ⁄ρ800,

hvor R = U ^ 2⁄P = 220 ^ 2⁄3146 = 15,3 Ohm, ρ800 = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (800-20) ∙11 ] = 1. 10 ^ (- 6) Ohm • m, lp = 15,3 ∙ 0,785 ∙ 10 ^ (- 6) ⁄ (1,11 ∙ 10 ^ (- 6)) = 10,9 m.

Også, hvis det er nødvendigt, i lighed med det første eksempel, kan D, h, n, lsp defineres.

Eksempel 3. Bestem den tilladte spænding for det rørformede elektriske varmelegeme (TEN).

Tilstand... Varmeelementets spiral er lavet af nichromtråd med diameter d = 0,28 mm og længde l = 4,7 m. Varmeelementet er i stille luft med en temperatur på 20 °C. Karakteristika for nichrom: ρ20 = 1,1 ∙ 10 ^ (- 6) Ohm • m; αр = 16 ∙ 10 ^ (- 6) 1 / ° C. Længden af ​​den aktive del af huset til varmeelementet er La = 40 cm.

Varmeelementet er glat, udvendig diameter dob = 16 mm. Varmeoverførselskoefficient α = 40 W / (m ^ 2 ∙ ° C). Termiske modstande: fyldstof RT3 = 0,3 ОС / W, husvægge Rт2 = 0,002 ОС / W.

Bestem, hvilken maksimal spænding der kan påføres varmeelementet, så dets spoletemperatur Tsp ikke overstiger 1000 ℃.

Svar. Varmeelementets temperatur på varmeelementet

Tsp = To + P ∙ (Rt1 + Rt2 + Rt3),

hvor det er den omgivende lufttemperatur; P er varmeelementets effekt, W; RT1 — termisk kontaktmodstand for rør-medium-grænsefladen.

Varmeelementets effekt P = U ^ 2⁄R,

hvor R er modstanden af ​​varmespiralen.Derfor kan vi skrive Tsp-To = U ^ 2 / R ∙ (Rt1 + Rt2 + Rt3), hvorfra spændingen på varmeelementet

U = √ ((R ∙ (Tsp-To)) / (Rt1 + Rt2 + Rt3)).

Find R = ρ ∙ (4 ∙ l) ⁄ (π ∙ d ^ 2),

hvor ρ1000 = ρ20 ∙ [1 + αp ∙ (T-20)] = 1,1 ∙ 10 ^ (- 6) ∙ [1 + 16 ∙ 10 ^ (- 6) ∙ (1000-20) ^∙ 12 ∙ — 6) Ohm • m.

Så R = 1,12 ∙ 10 ^ (- 6) ∙ (4 ∙ 4,7) ⁄ (3,14 ∙ (0,28 ∙ 10 ^ (- 3)) ^ 2) = 85,5 Ohm.

Kontakt termisk modstand RT1 = 1⁄ (α ∙ F),

hvor F er arealet af den aktive del af varmeelementets skal; F = π ∙ dob ∙ La = 3,14 ∙ 0,016 ∙ 0,4 = 0,02 m2.

Find Rt1 = 1⁄ (40 ∙ 0,02 = 1,25) OC / W.

Bestem spændingen på varmeelementet U = √ ((85,5 ∙ (1000-20)) / (1,25 + 0,002 + 0,3)) = 232,4 V.

Hvis den nominelle spænding angivet på varmelegemet er 220 V, vil overspændingen ved Tsp = 1000 OS være 5,6 % ∙ Un.