AC induktor

Overvej et kredsløb, der indeholder en induktor, og antag, at modstanden af ​​kredsløbet, inklusive spoleledningen, er så lille, at den kan negligeres. I dette tilfælde vil tilslutning af spolen til en jævnstrømskilde resultere i en kortslutning, hvor strømmen i kredsløbet som bekendt ville være meget stor.

Situationen er anderledes, når spolen er tilsluttet en AC-kilde. I dette tilfælde sker der ingen kortslutning. Dette viser. Hvad modstår en induktor over for vekselstrøm, der passerer gennem den.

Hvad er essensen af ​​denne modstand, og hvordan betinges den?

For at besvare dette spørgsmål, husk fænomenet selvinduktion… Enhver ændring i strøm i spolen forårsager, at en EMF af selvinduktion vises i den, som forhindrer en ændring i strøm. Værdien af ​​EMF af selvinduktion er direkte proportional med spolens induktansværdi og ændringshastigheden af ​​strømmen i den. Men siden vekselstrøm ændres kontinuerligt Den elektromagnetiske stråling til selvinduktion, der løbende optræder i spolen, skaber modstand mod vekselstrøm.

At forstå de processer, der foregår i vekselstrømkredsløb med induktoren, se grafen.Figur 1 viser buede linjer, der karakteriserer henholdsvis mærket i kredsløbet, spændingen i spolen og emk af selvinduktion, der forekommer i det. Lad os sikre os, at konstruktionerne i figuren er korrekte.

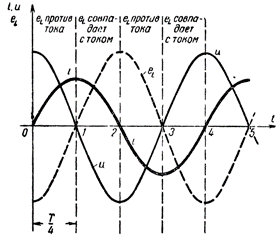
AC-kredsløb med en induktor

Fra det øjeblik t = 0, det vil sige fra det første øjeblik af observation af strømmen, begynder den at stige hurtigt, men når den nærmer sig sin maksimale værdi, falder stigningshastigheden af ​​strømmen. I det øjeblik, hvor strømmen nåede sin maksimale værdi, blev hastigheden af ​​dens ændring momentant lig med nul, det vil sige, at den aktuelle ændring stoppede. Så startede strømmen først langsomt og faldt derefter hurtigt, og efter periodens andet kvartal faldt den til nul. Ændringshastigheden af ​​strømmen i løbet af denne fjerdedel af perioden, stigende fra kuglen, når den højeste værdi, når strømmen bliver lig med nul.

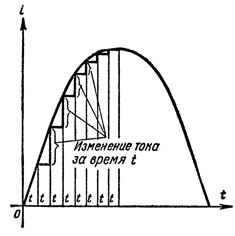
Figur 2. Arten af ​​ændringer i strømmen over tid, afhængig af strømmens størrelse

Ud fra konstruktionerne i figur 2 kan det ses, at når strømkurven passerer gennem tidsaksen, så stiger strømmen i et kort tidsrum T mere end i samme tidsrum, hvor strømkurven når sit højdepunkt.

Derfor falder strømmens ændringshastighed, når strømmen stiger, og stiger, når strømmen falder, uanset retningen af ​​strømmen i kredsløbet.

Det er indlysende, at emk af selvinduktansen i spolen skal være størst, når strømmens ændringshastighed er størst, og falde til nul, når dens ændring ophører. Faktisk, på grafen, faldt EMF-kurven for selvinduktion eL i første kvartal af perioden, startende fra den maksimale værdi, til nul (se fig. 1).

I løbet af det næste kvartal af perioden falder strømmen fra den maksimale værdi til nul, men hastigheden af ​​dens ændring stiger gradvist og er størst i det øjeblik, hvor strømmen er lig med nul. Følgelig stiger EMF for selvinduktionen i denne fjerdedel af perioden, der vises igen i spolen, gradvist og viser sig at være et maksimum, indtil strømmen bliver lig med nul.

Retningen af ​​selvinduktions-emk ændrede sig dog i den modsatte retning, da stigningen i strømmen i periodens første kvartal blev erstattet i andet kvartal af faldet.

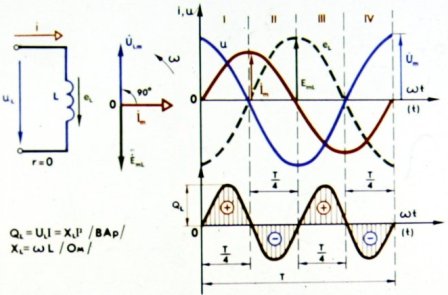
Kredsløb med induktans

Ved at fortsætte yderligere konstruktionen af ​​kurven for EMF for selvinduktion, er vi overbevist om, at i løbet af perioden med ændring af strøm i spolen og EMF af selvinduktion i den vil fuldføre en fuld periode med sin ændring. Dens retning er bestemt Lenz' lov: med en stigning i strømmen vil emf af selvinduktion være rettet mod strømmen (det første og tredje kvartal af perioden), og med et fald i strømmen, tværtimod, falder det sammen med det i retning ( andet og fjerde kvartal af perioden).

Derfor forhindrer EMF af selvinduktion forårsaget af selve vekselstrømmen den i at stige, og tværtimod opretholder den den, når den falder.

Lad os nu gå til spolens spændingsgraf (se fig. 1). I denne graf er sinusbølgen af ​​spoleterminalspændingen vist lig med og modsat sinusbølgen af ​​selvinduktansen emf. Derfor er spændingen ved spolens terminaler på ethvert tidspunkt lig og modsat EMF af selvinduktion, der opstår i den. Denne spænding er skabt af en generator og går til at slukke handlingen i EMF selvinduktionskredsløbet.

Derfor skabes modstand i en induktor forbundet med et AC-kredsløb, når strømmen løber. Men da en sådan modstand til sidst inducerer spolens induktans, så kaldes det induktiv modstand.

Induktiv modstand er betegnet med XL og måles som en modstand i ohm.

Kredsløbets induktive modstand er jo større, jo større aktuelle kildefrekvenskredsløbsforsyning og større kredsløbsinduktans. Derfor er den induktive modstand af et kredsløb direkte proportional med frekvensen af ​​strømmen og kredsløbets induktans; er bestemt af formlen XL = ωL, hvor ω — cirkulær frekvens bestemt af produktet 2πe... — kredsløbsinduktans i n.

Ohms lov for et AC-kredsløb, der indeholder en induktiv modstand lyder Således: strømmængden er direkte proportional med spændingen og omvendt proportional med den induktive modstand af NSi, dvs. I = U / XL, hvor I og U er de effektive strøm- og spændingsværdier, og xL er kredsløbets induktive modstand.

I betragtning af graferne for ændringen af ​​strøm i spolen. EMF af selvinduktion og spænding ved dets terminaler, vi var opmærksomme på, at ændringen i dem vVærdier ikke falder sammen i tid. Med andre ord viste strøm-, spændings- og selvinduktions-EMF-sinusoiderne sig at være tidsforskydne i forhold til hinanden for det pågældende kredsløb. I AC-teknologi kaldes dette fænomen almindeligvis for faseskift.

Hvis to variable størrelser ændrer sig i henhold til den samme lov (i vores tilfælde sinusformet) med de samme perioder, når deres maksimale værdi samtidig i både fremadgående og tilbagegående retning og samtidig falder til nul, så har sådanne variable størrelser de samme faser eller, som man siger, match i fase.

Som et eksempel viser figur 3 fasetilpassede strøm- og spændingskurver. Vi observerer altid sådan fasetilpasning i et AC-kredsløb, der kun består af aktiv modstand.

I det tilfælde, hvor kredsløbet indeholder induktiv modstand, strøm- og spændingsfaser, som det ses i fig. 1 stemmer ikke overens, det vil sige, at der er et faseskift mellem disse variable. Strømkurven ser i dette tilfælde ud til at halte efter spændingskurven med en fjerdedel af perioden.

Når en induktor indgår i et AC-kredsløb, sker der derfor en faseforskydning mellem strøm og spænding i kredsløbet, og strømmen halter spændingen i fase med en fjerdedel af perioden... Det betyder, at den maksimale strøm indtræder en fjerdedel af perioden efter at have nået den maksimale spænding.

Selvinduktionens EMF er i modfase med spolens spænding og halter efter strømmen med en fjerdedel af perioden. I dette tilfælde er perioden for ændring af strømmen, spændingen samt EMF for selvinduktion ændres ikke og forbliver lig med ændringsperioden for spændingen af ​​generatoren, der fodrer kredsløbet. Den sinusformede karakter af ændringen i disse værdier er også bevaret.

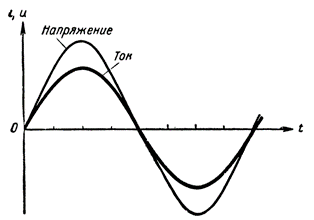
Figur 3. Fasetilpasning af strøm og spænding i et aktivt modstandskredsløb

Lad os nu forstå forskellen mellem en generatorbelastning med aktiv modstand og belastning med dens induktive modstand.

Når et AC-kredsløb kun indeholder én aktiv modstand, absorberes strømkildens energi i den aktive modstand, opvarmning af ledningen.

Når kredsløbet ikke indeholder aktiv modstand (vi betragter det normalt som nul), men kun består af induktiv modstand af spolen, bruges strømkildens energi ikke på opvarmning af ledningerne, men kun på at skabe en EMF af selvinduktion , det vil sige, at det bliver magnetfeltets energi ... Vekselstrømmen ændrer sig dog konstant både i størrelse og retning, og derfor, magnetfelt spolen ændrer sig løbende i takt med strømmen. I løbet af det første kvartal af perioden, hvor strømmen er stigende, modtager kredsløbet energi fra strømkilden og lagrer det i spolens magnetfelt. Men så snart strømmen, der har nået sit maksimum, begynder at falde, opretholdes den på bekostning af energien, der er lagret i spolens magnetfelt ved selvinduktionens emk.

Derfor modtager strømkilden, efter at have givet noget af sin energi til kredsløbet i første kvartal af perioden, den tilbage fra spolen i andet kvartal, der fungerer som en slags strømkilde. Med andre ord, et AC-kredsløb, der kun indeholder induktiv modstand, bruger ingen energi: i dette tilfælde er der en energiudsving mellem kilden og kredsløbet. Aktiv modstand absorberer tværtimod al den energi, der overføres til den fra den nuværende kilde.

En induktor siges, i modsætning til en ohmsk modstand, at være inaktiv med hensyn til en AC-kilde, dvs. reaktiv... Derfor kaldes spolens induktive modstand også for reaktans.

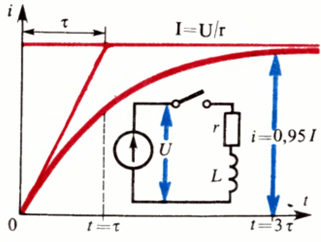
Strømstigningskurve ved lukning af et kredsløb, der indeholder en induktans — transienter i elektriske kredsløb.

Tidligere i denne tråd: Elektricitet til dummies / Grundlæggende om elektroteknik

Hvad læser andre?

# 1 Indsendt af: Alexander (4. marts 2010 17:45)

   
er strømmen i fase med generatorens emk? Og dens værdi falder?

#2 skrev: administrator (7. marts 2010 kl. 16.35)

   
I et AC-kredsløb, der kun består af aktiv modstand, passer strøm- og spændingsfaserne.
       

#3 skrev: Alexander (10. marts 2010 09:37)

   
Hvorfor er spændingen lig med og modsat selvinduktionens EMF, når alt kommer til alt, i det øjeblik, hvor EMF af selvinduktionen er maksimal, er generatorens EMF lig med nul og kan ikke skabe denne spænding? Hvor kommer (spændingen) fra?

* I et kredsløb med kun én induktor, der ikke har nogen aktiv modstand, er strømmen, der løber gennem kredsløbet i fase med generatorens emk (emk, som afhænger af rammepositionen (i en almindelig generator), ikke generatorspændingen)?