Beregninger til forbedring af effektfaktoren i et trefaset netværk

Når vi beregner kapacitansen af ​​en kondensator for at forbedre effektfaktoren i et trefaset netværk, vil vi overholde den samme sekvens som i artiklen med eksempler på beregninger i et enfaset netværk… Værdien af ​​effektfaktoren bestemmes af effektformlen for trefasestrøm:

P1 = √3 ∙ U ∙ I ∙ cosφ, cosφ = P1 / (√3 ∙ U ∙ I).

Eksempler på

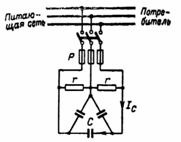
1. En trefaset induktionsmotor har følgende paneldata: P = 40 kW, U = 380 V, I = 105 A, η = 0,85, f = 50 Hz. Stjerneforbindelse af statoren. Antag, at det er svært at bestemme cosφ-værdien af ​​tavlen, og derfor er det nødvendigt at bestemme det. Til hvilken værdi vil strømmen falde efter forbedring af effektfaktoren til cosφ = 1 ved hjælp af kondensatorer? Hvilken kapacitet skal kondensatorerne have? Hvilken reaktiv effekt vil kondensatorerne (fig. 1) kompensere for?

Statorviklingens klemmer er markeret: start — C1, C2, C3, ender — henholdsvis C4, C5, C6.I det følgende vil oprindelsen dog for at lette kommunikationen med diagrammerne blive mærket A, B, C og enderne X, Y, Z.

Ris. 1.

Motoreffekt P1 = P2 / η = 40000 / 0,85 ≈47000 W,

hvor P2 er den nettoeffekt, der er angivet på motorens typeskilt.

cosφ = P1 / (√3 ∙ U ∙ I) = 47000 / (√3 ∙ 380 ∙ 105) = 0,69.

Efter at have forbedret effektfaktoren til cosφ = 1, vil indgangseffekten være:

P1 = √3 ∙ U ∙ I ∙ 1

og strømmen falder til

I1 = P1 / (√3 ∙ U) = 47000 / (1,73 ∙ 380) = 71,5 A.

Dette er den aktive strøm ved cosφ = 0,69 siden

Ia = I ∙ cosφ = 105 ∙ 0,69 = 71,5 A.

I fig. 1 viser inklusion af kondensatorer for at forbedre cosφ.

Kondensatorspænding Uph = U / √3 = 380 / √3 = 220 V.

Fasemagnetiseringsstrømmen er lig med den lineære magnetiseringsstrøm: IL = I ∙ sinφ = 105 ∙ 0,75 = 79,8 A.

Den kapacitive modstand af kondensatoren, som skal levere magnetiseringsstrømmen, vil være: xC = Uph / IL = 1 / (2 ∙ π ∙ f ∙ C).

Derfor er kapacitansen af ​​kondensatoren C = IC / (Uph ∙ 2 ∙ π ∙ f) = 79,8 / (220 ∙ 3,14 ∙ 100) = 79,800 / (22 ∙ 3,14) = ∙ 16,0 = 16,0

En blok af kondensatorer med en samlet kapacitet på C = 3 ∙ 1156,4≈3469 μF skal tilsluttes en trefaset motor for at forbedre effektfaktoren til cosφ = 1 og samtidig reducere strømmen fra 105 til 71,5 A.

Den samlede reaktive effekt kompenseret af kondensatorer, som i mangel af kondensatorer tages fra netværket, Q = 3 ∙ Uph ∙ IL = 3 ∙ 220 ∙ 79,8≈52668 = 52,66 kvar.

I dette tilfælde bruger motoren kun aktiv effekt P1 = 47 kW fra netværket.

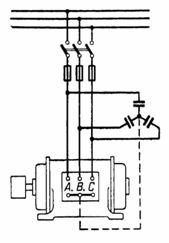
I fig.2 viser en blok af kondensatorer forbundet i et delta og forbundet med terminalerne på en trefaset motor, hvis vikling også er forbundet i en delta. Denne forbindelse af kondensatorer er mere fordelagtig end forbindelsen vist i fig. 1 (se konklusionen på beregning 2).

Ris. 2.

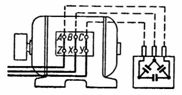
2. Et lille kraftværk forsyner et trefaset netværk med en strøm I = 250 A ved en netværksspænding U = 380 V og en netværkseffektfaktor cosφ = 0,8. Forbedringen af ​​effektfaktoren opnås af kondensatorer, som er tilsluttet i delta ifølge diagrammet i fig. 3. Det er nødvendigt at bestemme værdien af ​​kondensatorernes kapacitans og den kompenserede reaktive effekt.

Ris. 3.

Tilsyneladende effekt S = √3 ∙ U ∙ I = 1,73 ∙ 380 ∙ 250 = 164,3 kVA.

Bestem den aktive effekt ved cosφ = 0,8:

P1 = √3 ∙ U ∙ I ∙ cosφ = S ∙ cosφ≈164,3 ∙ 0,8 = 131,5 W.

Reaktiv effekt skal kompenseres ved cosφ = 0,8

Q = S ∙ sinφ≈164,3 ∙ 0,6 = 98,6 kvar.

Derfor er den lineære magnetiseringsstrøm (fig. 3) IL = I ∙ sinφ = Q / (√3 ∙ U) ≈150 A.

Magnetiserende (kapacitiv) fasestrøm ICph = Q / (3 ∙ U) = 98580 / (3 ∙ 380) = 86,5 A.

Kondensatorstrømmen kan bestemmes på en anden måde ved den magnetiserende (reaktive) strøm i kredsløbet:

IL = I ∙ sinφ = 250 ∙ 0,6 = 150 A,

ICph = ILph = IL / √3 = 150 / 1,73 = 86,7 A.

Når de er tilsluttet i et delta, har hver gruppe af kondensatorer en spænding på 380 V og en fasestrøm ICph = 86,7 A.

I = ICf = U / xC = U / (1⁄ (ω ∙ C)) = U ∙ ω ∙ C.

Derfor er C = IC / (U ∙ 2 ∙ π ∙ f) = 86,7 / (300 ∙ π ∙ 100) = 726 μF.

Den samlede kapacitans af kondensatorbanken er C3 = 3 ∙ 726 = 2178 μF.

De tilsluttede kondensatorer gør det muligt at bruge hele kraftværkets effekt S = 164,3 kVA i form af nettoeffekt.Uden driftskondensatorer bruges kun aktiv effekt på 131,5 kW ved cosφ = 0,8.

Den kompenserede reaktive effekt Q = 3 ∙ U ∙ IC = 3 ∙ ω ∙ C ∙ U ^ 2 stiger i forhold til kvadratet af spændingen. Derfor er den nødvendige kapacitet af kondensatorerne, og dermed omkostningerne til kondensatorerne, lavere, fordi spændingen er højere.

Modstande r i fig. 3 bruges til gradvist at aflade kondensatorer, når de er afbrudt fra netværket.